【题目】如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB﹣BD做匀速运动,动点Q从点D同时出发,沿着线路DC﹣CB﹣BA做匀速运动.

(1)求BD的长;
(2)已知动点P、Q运动的速度分别为8cm/s、10cm/s.经过12秒后,P、Q分别到达M、N两点,试判断△AMN的形状,并说明理由,同时求出△AMN的面积;
(3)设问题(2)中的动点P、Q分别从M、N同时沿原路返回,动点P的速度不变,动点Q的速度改变为a cm/s,经过3秒后,P、Q分别到达E、F两点,若△BEF为直角三角形,试求a的值.
参考答案:
【答案】(1)48cm;(2)288![]() (cm2);(3)若△BEF为直角三角形,a的值为4或12或24.
(cm2);(3)若△BEF为直角三角形,a的值为4或12或24.
【解析】
试题分析:(1)根据菱形的性质得AB=BC=CD=AD=48,加上∠A=60°,于是可判断△ABD是等边三角形,所以BD=AB=48;
(2)如图1,根据速度公式得到12秒后点P走过的路程为96cm,则点P到达点D,即点M与D点重合,12秒后点Q走过的路程为120cm,而BC+CD=96,易得点Q到达AB的中点,即点N为AB的中点,根据等边三角形的性质得MN⊥AB,即△AMN为直角三角形,然后根据等边三角形面积可计算出S△AMN=288![]() cm2;
cm2;
(3)由△ABD为等边三角形得∠ABD=60°,根据速度公式得经过3秒后点P运动的路程为24cm、点Q运动的路程为3acm,所以BE=DE=24cm,
然后分类讨论:当点Q运动到F点,且点F在NB上,如图1,则NF=3a,BF=BN﹣NF=24﹣3a,由于△BEF为直角三角形,而∠FBE=60°,只能得到∠EFB=90°,所以∠FEB=30°,根据含30度的直角三角形三边的关系得24﹣3a=![]() ×24,解得a=4;当点Q运动到F点,且点F在BC上,如图2,则NF=3a,BF=BN﹣NF=3a﹣24,由于△BEF为直角三角形,而∠FBE=60°,若∠EFB=90°,则∠FEB=30°,根据含30度的直角三角形三边的关系得3a﹣24=
×24,解得a=4;当点Q运动到F点,且点F在BC上,如图2,则NF=3a,BF=BN﹣NF=3a﹣24,由于△BEF为直角三角形,而∠FBE=60°,若∠EFB=90°,则∠FEB=30°,根据含30度的直角三角形三边的关系得3a﹣24=![]() ×24,解得a=12;若∠EFB=90°,易得此时点F在点C处,则3a=24+48,解得a=24.
×24,解得a=12;若∠EFB=90°,易得此时点F在点C处,则3a=24+48,解得a=24.
解:(1)∵四边形ABCD是菱形,
∴AB=BC=CD=AD=48,
∵∠A=60°,
∴△ABD是等边三角形,
∴BD=AB=48,
即BD的长是48cm;
(2)如图1,12秒后点P走过的路程为8×12=96,则12秒后点P到达点D,即点M与D点重合,
12秒后点Q走过的路程为10×12=120,而BC+CD=96,所以点Q到B点的距离为120﹣96=24,则点Q到达AB的中点,即点N为AB的中点,
∵△ABD是等边三角形,而MN为中线,
∴MN⊥AB,
∴△AMN为直角三角形,
∴S△AMN=![]() S△ABD=
S△ABD=![]() ×
×![]() ×482=288
×482=288![]() (cm2);
(cm2);
(3)∵△ABD为等边三角形,
∴∠ABD=60°,
经过3秒后,点P运动的路程为24cm、点Q运动的路程为3acm,
∵点P从点M开始运动,即DE=24cm,
∴点E为DB的中点,即BE=DE=24cm,
当点Q运动到F点,且点F在NB上,如图1,则NF=3a,
∴BF=BN﹣NF=24﹣3a,
∵△BEF为直角三角形,
而∠FBE=60°,
∴∠EFB=90°(∠FEB不能为90°,否则点F在点A的位置),
∴∠FEB=30°,
∴BF=![]() BE,
BE,
∴24﹣3a=![]() ×24,
×24,
∴a=4;
当点Q运动到F点,且点F在BC上,如图2,则NF=3a,
∴BF=BN﹣NF=3a﹣24,
∵△BEF为直角三角形,
而∠FBE=60°,
若∠EFB=90°,则∠FEB=30°,
∴BF=![]() BE,
BE,
∴3a﹣24=![]() ×24,
×24,
∴a=12;
若∠EFB=90°,即FB⊥BD,
而DE=BE,
∴点F在BD的垂直平分线上,
∴此时点F在点C处,
∴3a=24+48,
∴a=24,
综上所述,若△BEF为直角三角形,a的值为4或12或24.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.

(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点分别为A(-2,2),B(0,5),C(0,2).
(1)画△
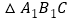 ,使它与△ABC关于点C成中心对称;
,使它与△ABC关于点C成中心对称;(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),画出平移后对应的
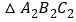 ;
;(3)若将
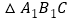 绕某一点旋转可得到
绕某一点旋转可得到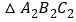 ,则旋转中心的坐标为 _____________.
,则旋转中心的坐标为 _____________.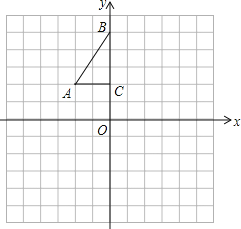
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
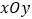 中,正比例函数
中,正比例函数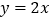 与反比例函数
与反比例函数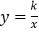 的图象交于A,B两点,A点的横坐标为2,AC⊥x轴于点C,连接BC.
的图象交于A,B两点,A点的横坐标为2,AC⊥x轴于点C,连接BC.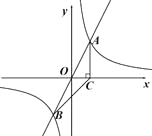
(1)求反比例函数的解析式;
(2)若点P是反比例函数
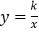 图象上的一点,且满足△OPC与△ABC的面积相等,请直接写出点P的坐标.
图象上的一点,且满足△OPC与△ABC的面积相等,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(a,0),B(0,b),且a、b满足
 =0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线
=0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线 经过C、D两点.
经过C、D两点. (1)求k的值;
(2)点P在双曲线
 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,
 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.

(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司员工分别住在A、B、C、D四个住宅区,A区有20人,B区有15人,C区有5人,D区有30人,四个区在同一条直线上,位置如图所示.该公司的接送车打算在此间设立一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设置在( )

A. D区 B. A区 C. AB两区之间 D. BC两区之间
相关试题

