【题目】已知直线y=﹣ ![]() x+3与坐标轴分别交于点A,B,点P在抛物线y=﹣
x+3与坐标轴分别交于点A,B,点P在抛物线y=﹣ ![]() (x﹣
(x﹣ ![]() )2+4上,能使△ABP为等腰三角形的点P的个数有( )
)2+4上,能使△ABP为等腰三角形的点P的个数有( )
A.3个
B.4个
C.5个
D.6个
参考答案:
【答案】A
【解析】解:以点B为圆心线段AB长为半径作圆,交抛物线于点C、M、N点,连接AC、BC,如图所示.
令一次函数y=﹣ ![]() x+3中x=0,则y=3,
x+3中x=0,则y=3,
∴点A的坐标为(0,3);
令一次函数y=﹣ ![]() x+3中y=0,则﹣
x+3中y=0,则﹣ ![]() x+3=0,
x+3=0,
解得:x= ![]() ,
,
∴点B的坐标为( ![]() ,0).
,0).
∴AB=2 ![]() .
.
∵抛物线的对称轴为x= ![]() ,
,
∴点C的坐标为(2 ![]() ,3),
,3),
∴AC=2 ![]() =AB=BC,
=AB=BC,
∴△ABC为等边三角形.
令y=﹣ ![]() (x﹣
(x﹣ ![]() )2+4中y=0,则﹣
)2+4中y=0,则﹣ ![]() (x﹣
(x﹣ ![]() )2+4=0,
)2+4=0,
解得:x=﹣ ![]() ,或x=3
,或x=3 ![]() .
.
∴点E的坐标为(﹣ ![]() ,0),点F的坐标为(3
,0),点F的坐标为(3 ![]() ,0).
,0).
△ABP为等腰三角形分三种情况:①当AB=BP时,以B点为圆心,AB长度为半径做圆,与抛物线交于C、M、N三点;②当AB=AP时,以A点为圆心,AB长度为半径做圆,与抛物线交于C、M两点,;③当AP=BP时,作线段AB的垂直平分线,交抛物线交于C、M两点;
∴能使△ABP为等腰三角形的点P的个数有3个.
故选A.
以点B为圆心线段AB长为半径作圆,交抛物线于点C、M、N点,连接AC、BC,由直线y=﹣ ![]() x+3可求出点A、B的坐标,结合抛物线的解析式可得出△ABC等边三角形,再令抛物线解析式中y=0求出抛物线与x轴的两交点的坐标,发现该两点与M、N重合,结合图形分三种情况研究△ABP为等腰三角形,由此即可得出结论.
x+3可求出点A、B的坐标,结合抛物线的解析式可得出△ABC等边三角形,再令抛物线解析式中y=0求出抛物线与x轴的两交点的坐标,发现该两点与M、N重合,结合图形分三种情况研究△ABP为等腰三角形,由此即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,∠A=30°.

(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是直线,O是AB上一点,∠AOE是直角,∠FOD=90°,OB平分∠DOC,则图中与∠DOE互余的角有__________个;与∠DOE互补的角有___________个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=_____°,射线OC的方向是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用边长为12cm的正方形硬纸板做三棱柱盒子,每个盒子的侧面为长方形,底面为等边三角形.
(1)每个盒子需 个长方形, 个等边三角形;
(2)硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面.

现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
① 用x的代数式分别表示裁剪出的侧面和底面的个数;
② 若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
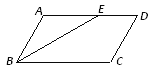
查看答案和解析>>【题目】平行四边形ABCD中,∠ABC的角平分线BE将边AD分成长度为5cm和6cm的两部分,则平行四边形ABCD的周长为__________________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)
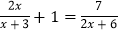
(2)
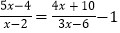
相关试题

