【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象交于点
的图象交于点![]() .
.
(![]() )
)![]() __________;
__________;![]() __________.
__________.
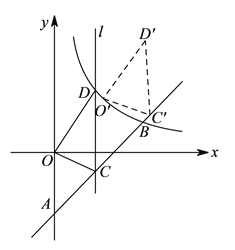
(![]() )点
)点![]() 是直线
是直线![]() 上的动点(与点
上的动点(与点![]() ,
,![]() 不重合),过点
不重合),过点![]() 且平行于
且平行于![]() 轴的直线
轴的直线![]() 交这个反比例函数的图象于点
交这个反比例函数的图象于点![]() ,当点
,当点![]() 的横坐标为
的横坐标为![]() 时,得
时,得![]() ,现将
,现将![]() 沿射线
沿射线![]() 方向平移一定的距离(如图),得到
方向平移一定的距离(如图),得到![]() ,若点
,若点![]() 的对应点
的对应点![]() 落在该反比例函数图象上,求点
落在该反比例函数图象上,求点![]() ,
,![]() 的坐标.
的坐标.
参考答案:
【答案】(![]() )
)![]() ,
,![]() ;(
;(![]() )
)![]() ,
,![]()
【解析】试题分析:(1)由点B的横坐标利用反比例函数图象上点的坐标特征即可求出b值,进而得出点B的坐标,再将点B的坐标代入一次函数解析式中即可求出k值;(2)由![]() 的横坐标为
的横坐标为![]() ,代入
,代入![]() ,得
,得![]() 、D的坐标,根据平移的性质即可找出点O′、D′的坐标.
、D的坐标,根据平移的性质即可找出点O′、D′的坐标.
试题解析:(![]() )
)![]() 在
在![]() 上,将
上,将![]() 代入
代入![]() ,得
,得![]() ,
,
∴![]() 又在
又在![]() 上,
上,
∴又![]() ,
,![]() .
.
(![]() )
)![]() 的横坐标为
的横坐标为![]() ,代入
,代入![]() ,得
,得![]() ,
,![]() 轴,
轴,
∴![]() 点横坐标为
点横坐标为![]() ,代入
,代入![]() 中,
中,
∴![]() .
.
∵平移,
∴![]() ≌
≌![]() ,设
,设![]() ,
,
∴![]() 在
在![]() 上,
上,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:
如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接A B′与直线l交于点C,则点C即为所求.
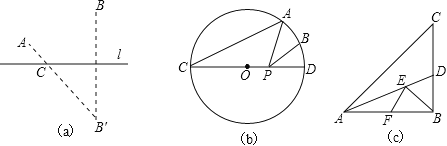
(1)实践运用:
如图(b),已知,⊙O的直径CD为4,点A 在⊙O 上,∠ACD=30°,B 为弧AD 的中点,P为直径CD上一动点,则BP+AP的最小值为 .
(2)知识拓展:
如图(c),在Rt△ABC中,AB=10,∠BAC=45°,∠BAC的平分线交BC于点D,E、F分别是线段AD和AB上的动点,求BE+EF的最小值,并写出解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将命题“同角的余角相等”改成“如果...,那么....”的形式.如果____________,那么______________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】∠A的两边与∠B的两边分别平行,∠A=50°,则∠B的度数为 ____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,Rt△ABC中,∠ACB=90。 , 直角边AC在射线OP上,直角顶点C与射线端点0重合,AC=b,BC=a,且满足
 .
.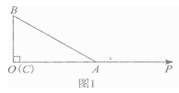
(1)求a,b的值;
(2)如图2,向右匀速移动Rt△ABC,在移动的过程中Rt△ABC的直角边AC在射线OP上匀速向右运动,移动的速度为1个单位/秒,移动的时间为t秒,连接OB,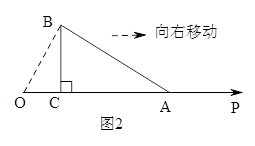
①若△OAB为等腰三角形,求t的值;
②Rt△ABC在移动的过程中,能否使△OAB为直角三角形?若能,求出t的值:若不能,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中
①无理数都是无限小数;
②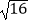 的平方根是±4;
的平方根是±4;
③无理数与数轴上的点一一对应;
④﹣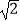 <﹣
<﹣  ;
;
正确的语句个数是( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,设每千克应涨价x元,则可列方程为
相关试题

