【题目】为创建“美丽乡村”,某村计划购买甲、乙两种树苗共400棵,对本村道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元.
![]() 若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?
若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?
![]() 若购买甲种树苗的金额不少于购买乙种树苗的金额,则至少应购买甲种树苗多少棵?
若购买甲种树苗的金额不少于购买乙种树苗的金额,则至少应购买甲种树苗多少棵?
参考答案:
【答案】(1)购买甲种树苗300棵,乙种树苗100棵;(2)至少应购买甲种树苗240棵.
【解析】
![]() 根据题意可以列出相应的方程组,从而可以求得需购买甲、乙两种树苗各多少棵;
根据题意可以列出相应的方程组,从而可以求得需购买甲、乙两种树苗各多少棵;
![]() 根据题意可以列出相应的不等式,从而可以求得至少应购买甲种树苗多少棵.
根据题意可以列出相应的不等式,从而可以求得至少应购买甲种树苗多少棵.
解:![]() 设购买甲种树苗x棵,乙种树苗y棵,
设购买甲种树苗x棵,乙种树苗y棵,
由题意得![]() ,
,
解得![]() ,
,
即购买甲种树苗300棵,乙种树苗100棵;
![]() 设购买甲种树苗a棵,
设购买甲种树苗a棵,
由题意得:![]() ,
,
解得:![]() ,
,
即至少应购买甲种树苗240棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求证:BE=AD;

(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=
 CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.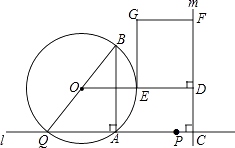
(1)用关于x的代数式表示BQ,DF.
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知两点A(3,0),B(0,4),点C在第一象限,AB⊥BC,BC=BA,点P在线段OB上,OP=OA,AP的延长线与CB的延长线交于点M,AB与CP交于点N.

(1)点C的坐标为: ;
(2)求证:BM=BN;
(3)设点C关于直线AB的对称点为D,点C关于直线AP的对称点为G,求证:D,G关于x轴对称.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
 ,点
,点 是直线
是直线 上一个动点(不与
上一个动点(不与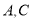 重合),点
重合),点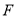 是
是 边上一个定点, 过点
边上一个定点, 过点 作
作 ,交直线
,交直线 于点
于点 ,连接
,连接 ,过点
,过点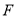 作
作 ,交直线
,交直线 于点
于点 .
.  如图①,当点
如图①,当点 在线段
在线段 上时,求证:
上时,求证: .
. 
 在
在 的条件下,判断
的条件下,判断 这三个角的度数和是否为一个定值? 如果是,求出这个值,如果不是,说明理由.
这三个角的度数和是否为一个定值? 如果是,求出这个值,如果不是,说明理由.  如图②,当点
如图②,当点 在线段
在线段  的延长线上时,(2)中的结论是否仍然成立?如果不成立, 请直接写出
的延长线上时,(2)中的结论是否仍然成立?如果不成立, 请直接写出 之间的关系.
之间的关系. )当点
)当点 在线段
在线段 的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接 写出
的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接 写出 之间的关系.
之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个一次函数
 和
和 的图象在同一坐标系内大致位置正确的是( )
的图象在同一坐标系内大致位置正确的是( )A.
 B.
B.  C.
C.  D.
D. 
相关试题

