【题目】如图,四边形ABCD中,AE平分∠BAD,DE平分∠ADC. 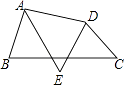
(1)如果∠B+∠C=120°,则∠AED的度数= . (直接写出结果)
(2)根据(1)的结论,猜想∠B+∠C与∠AED之间的关系,并证明.
参考答案:
【答案】
(1)60°
(2)解:∠AED= ![]() (∠B+∠C).
(∠B+∠C).
理由如下:在四边形ABCD中,
∵∠BAD+∠CDA+∠B+∠C=360°,
∴∠BAD+∠CDA=360°﹣(∠B+∠C),
又∵AE平分∠BAD,DE平分∠ADC,
∴∠EAD= ![]() ∠BAD,∠EDA=
∠BAD,∠EDA= ![]() ∠ADC,
∠ADC,
∴∠EAD+∠EDA= ![]() ∠BAD+
∠BAD+ ![]() ∠ADC=
∠ADC= ![]() [360°﹣(∠B+∠C)],
[360°﹣(∠B+∠C)],
在△AED中,又∵∠AED=180°﹣(∠EAD+∠EDA),
=180°﹣ ![]() [360°﹣(∠B+∠C)],
[360°﹣(∠B+∠C)],
= ![]() (∠B+∠C),
(∠B+∠C),
故∠AED= ![]() (∠B+∠C).
(∠B+∠C).
【解析】解:(1)在四边形ABCD中,∵∠B+∠C=120°, ∴∠BAD+∠CDA=360°﹣120°=240°,
∵AE平分∠BAD,DE平分∠ADC,
∴∠EAD= ![]() ∠BAD,∠EDA=
∠BAD,∠EDA= ![]() ∠ADC,
∠ADC,
∴∠EAD+∠EDA= ![]() ∠BAD+
∠BAD+ ![]() ∠ADC=
∠ADC= ![]() (∠BAD+∠CDA)=
(∠BAD+∠CDA)= ![]() ×240°=120°,
×240°=120°,
在△AED中,∠AED=180°﹣(∠EAD+∠EDA),
=180°﹣120°,
=60°;
所以答案是:60°.
【考点精析】本题主要考查了多边形内角与外角的相关知识点,需要掌握多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一个图形整体沿着某一直线方向移动,会得到一个新的图形,这种移动就叫做_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个相似三角形的周长之比为1∶4,则它们的面积之比为( )
A.1∶2B.1∶4C.1∶8D.1∶16
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)3x=-9x-12;
(2)2 ( 3 y 5 ) = 3 ( 1 y ) + 1;
(3)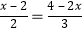 ;
;
(4)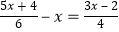 .
.
(1)3x=-9x-12
(2)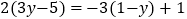
(3)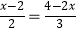
(4)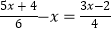
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强市民的节水意识,某市对居民用水实行“阶梯收费”.规定每户每月不超过月用水标准量部分的水价为1.5元/吨,超过月用水标准量部分的水价为2.5元/吨.该市小明家5月份用水12吨,交水费20元,该市规定的每户月用水标准量是多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣9= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC的垂直平分线分别交AC、BC于E、D两点,△ABC的周长为23,ABD的周长为15,则EC的长是( )

A.3
B.4
C.6
D.8
相关试题

