【题目】如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论错误的是( )
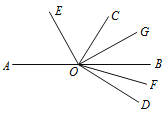
A. ∠DOG与∠BOE互补 B. ∠AOE-∠DOF=45°
C. ∠EOD与∠COG互补 D. ∠AOE与∠DOF互余
参考答案:
【答案】D
【解析】
根据角平分线的定义可设∠AOE=∠COE=α,∠BOG=∠COG=β,利用平角等于得出α+β=90°,∠EOG=90°.根据同角的余角相等得出∠DOG=∠COE=90°-∠COG=α,则∠BOD=∠DOG-∠BOG=α-β.∠BOF=∠DOF=![]() (α-β).然后根据互余、互补的定义分别判断即可.
(α-β).然后根据互余、互补的定义分别判断即可.
解:∵OE平分∠AOC,OG平分∠BOC,
∴可设∠AOE=∠COE=α,∠BOG=∠COG=β,
∵O为直线AB上一点,
∴∠AOB=180°,
∴2α+2β=180°,
∴α+β=90°,∠EOG=90°.
∵∠DOC=90°,
∴∠DOG=∠COE=90°-∠COG=α,
∴∠BOD=∠DOG-∠BOG=α-β.
∵OF平分∠BOD,
∴∠BOF=∠DOF=![]() (α-β).
(α-β).
A、∵∠DOG=α=∠AOE,∠AOE+∠BOE=180°,
∴∠DOG+∠BOE=180°,
故本选项结论正确,不符合题意;
B、∵∠AOE=α,∠DOF=![]() (α-β),
(α-β),
∴∠AOE-∠DOF=α-![]() (α-β)=
(α-β)=![]() (α+β)=45°,
(α+β)=45°,
故本选项结论正确,不符合题意;
C、∵∠EOD=∠EOG+∠GOD=90°+α,∠COG=β,
∴∠EOD+∠COG=90°+α+β=180°,
故本选项结论正确,不符合题意;
D、∵∠AOE+∠DOF=α+![]() (α-β)=
(α-β)=![]() α-
α-![]() β=
β=![]() α-
α-![]() (90°-α)=2α-45°,
(90°-α)=2α-45°,
∴当α=67.5°时,∠AOE+∠DOF=90°,
但是题目没有α=67.5°的条件,
故本选项结论错误,符合题意;
故选:D.
-
科目: 来源: 题型:
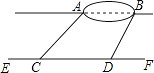
查看答案和解析>>【题目】小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解南山荔枝的销售情况,某部门对该市场的三种荔枝品种A,B,C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整),请你结合图中的信息,解答下列问题:

(1)该市场6月上半月共销售这三种荔枝多少吨?
(2)补全图1的统计图并计算图2中A所在扇形的圆心角的度数;
(3)某商场计划六月下半月进货A、B、C三种荔枝共300千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理? -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的⊙O过点E.
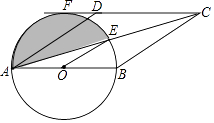
(1)求证:四边形ABCD的是菱形;
(2)若CD的延长线与圆相切于点F,已知直径AB=4,求阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校招聘一名数学老师,对应聘者分别进行了教学能力、科研能力和组织能力三项测试,其中甲、乙两名应聘者的成绩如右表:(单位:分)
教学能力
科研能力
组织能力
甲
81
85
86
乙
92
80
74
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?
(2)根据实际需要,学校将教学、科研和组织能力三项测试得分按 5:3:2 的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营A种品牌的玩具,购进时间的单价是30元,但据市场调查,在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请用含x的代数式表示该玩具的销售量;
(2)若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于450件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
(3)该商场计划将(2)中所得的利润的一部分资金采购一批B种玩具并转手出售,根据市场调查并准备两种方案,方案①:如果月初出售,可获利15%,并可用本和利再投资C种玩具,到月末又可获利10%;方案②:如果只到月末出售可直接获利30%,但要另支付他库保管费350元,请问商场如何使用这笔资金,采用哪种方案获利较多? -
科目: 来源: 题型:
查看答案和解析>>【题目】某河道A,B两个码头之间有客轮和货轮通行
 一天,客轮从A码头匀速行驶到B码头,同时货轮从
一天,客轮从A码头匀速行驶到B码头,同时货轮从B码头出发,运送一批建材匀速行驶到A码头
 两船距B码头的距离
两船距B码头的距离 千米
千米 与行驶时间
与行驶时间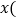 分
分 之间的函数关系
之间的函数关系如图所示
 请根据图象解决下列问题:
请根据图象解决下列问题: 分别求客轮和货轮距B码头的距离
分别求客轮和货轮距B码头的距离 千米
千米 、
、 千米
千米 与
与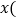 分
分 之间的函数关系式;
之间的函数关系式; 求点M的坐标,并写出该点坐标表示的实际意义.
求点M的坐标,并写出该点坐标表示的实际意义.
相关试题

