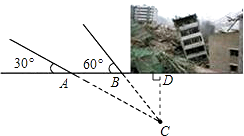
【题目】某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A,B相距3米,探测线与地面的夹角分别是30°和60°(如图),试确定生命所在点C的深度.(结果保留根号)
参考答案:
【答案】解:如图,过点C作CD⊥AB交AB的延长线于D点.
∵探测线与地面的夹角为30°和60°,
∴∠CAD=30°∠CBD=60°,
根据三角形的外角定理,得∠BCA=∠CBD﹣∠CAD=30°,
即∠BCA=∠CAD=30°,
∴BC=AB=3米,
在Rt△BDC中,CD=BCsin60°=3× ![]() =
= ![]() 米.
米.
答:生命所在点C的深度约为 ![]() 米.
米.
【解析】过点C作CD⊥AB交AB的延长线于D点,依据题意可得到∠CAD=30°,∠CBD=60°,接下来,依据三角形的外角的性质可求得∠BCA=30°,则BC=AB=3米,最后,在Rt△BDC中利用特殊锐角三角函数值求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在梯形ABCD中,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.
求证:CE⊥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④BD平分∠ADC;⑤∠BDC=
 ∠BAC.
∠BAC.
其中正确的结论有( )
A. 5个 B. 4个
C. 3个 D. 2个
-
科目: 来源: 题型:
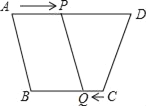
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=8cm,P,Q分别从A,C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C出发向B运动,_____秒后四边形ABQP是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5).
(1)求此一次函数的表达式;
(2)若点P为此一次函数图象上一点,且△POB的面积为10,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若我们规定三角“
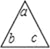 ”表示为:abc;方框“
”表示为:abc;方框“ ”表示为:(xm+yn).例如:
”表示为:(xm+yn).例如: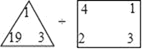 =1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
=1×19×3÷(24+31)=3.请根据这个规定解答下列问题:(1)计算:
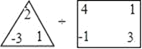 = ______ ;
= ______ ;(2)代数式
 为完全平方式,则k= ______ ;
为完全平方式,则k= ______ ;(3)解方程:
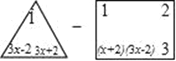 =6x2+7.
=6x2+7. -
科目: 来源: 题型:
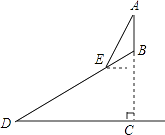
查看答案和解析>>【题目】某山的山顶B处有一个观光塔,已知该山的山坡面与水平面的夹角∠BDC为30°,山高BC为100米,点E距山脚D处150米,在点E处测得观光塔顶端A的仰角为60°,则观光塔AB的高度是( )
A.50米
B.100米
C.125米
D.150米
相关试题

