Question

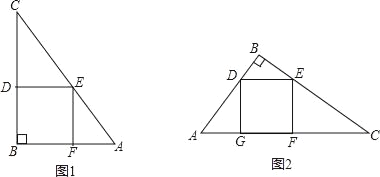
【题目】一块直角三角形木板的一条直角边AB长为1.5m，面积为1.5m2，工人师傅要把它加工成一个面积最大的正方形桌面，请甲、乙两位同学进行设计加工方案，甲设计方案如图1，乙设计方案如图2．你认为哪位同学设计的方案较好？试说明理由．（加工损耗忽略不计，计算结果中可保留分数）

Answer 1

【答案】甲同学设计的方案较好

【解析】试题分析：利用正方形的对边平行．寻找相似三角形，由“相似三角形对应边的比，等于对应边上高的比”的性质，列出等量关系，计算正方形的边长x、y，比较大小，选择合理方案．

试题解析：解：由AB=1.5m，S△ABC=1.5m2，可得BC=2m．

由图1，若设甲设计的正方形桌面边长为xm，由DE∥AB，得Rt△CDE∽Rt△CBA，

∴，即，∴3﹣1.5x=2x，x=．

由图2，过点B作Rt△ABC斜边AC上的高，BH交DE于P，交AC于H．

由AB=1.5m，BC=2m，得AC===2.5（m）．

由ACBH=ABBC可得，BH===1.2m．

设乙设计的桌面的边长为ym．

∵DE∥AC，∴Rt△BDE∽Rt△BAC，∴ ，即，解得y=．

∵=＞，∴x2＞y2，∴甲同学设计的方案较好．