【题目】如图,数轴上A、B两点分别对应有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|,利用数形结合思想回答下列问题:![]()
(1)数轴上表示2和10两点之间的距离是____,数轴上表示2和-10两点之间的距离是
____;
(2)数轴上,x和-2两点之间的距离是|x+2|_____;
(3)若x表示一个有理数,则|x-1+|x+2|有最小值吗?若有,请求出最小值,若没有,写出理由.
参考答案:
【答案】(1) 8,12;;(2) |x+2|;(3)最小值为3.
【解析】
(1)结合数轴即可求距离;
(2)由绝对值的性质可以表示x与-2之间的距离为|x+2|;
(3)当-2<x<1时有最小值,最小值就是1与-2之间的距离.
(1)2与10之间的距离是8,2与-10之间的距离是12,
故答案为8,12;
(2)表示x与-2之间的距离为|x+2|,
故答案为|x+2|;
(3)|x-1+|x+2|表示数轴上x与1的两点之间与x和-2的两点之间的距离和,
利用数轴就可以发现:当-2<x<1时有最小值,最小值就是1与-2之间的距离,
即|x-1+|x+2|的最小值为3.
-
科目: 来源: 题型:
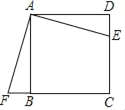
查看答案和解析>>【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)求证:△ADE≌△ABF.
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到.
-
科目: 来源: 题型:
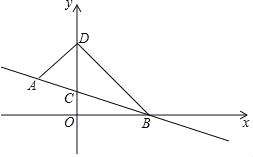
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB过点A(﹣1,1),B(2,0),交y轴于点C,点D (0,n)在点C上方.连接AD,BD.
(1)求直线AB的关系式;
(2)求△ABD的面积;(用含n的代数式表示)
(3)当S△ABD=2时,作等腰直角三角形DBP,使DB=DP,求出点P的坐标.
-
科目: 来源: 题型:
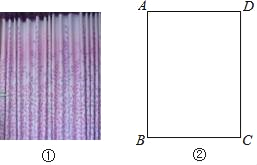
查看答案和解析>>【题目】如图①,窗帘的褶皱是指按照窗户的实际宽度将窗帘布料以一定比例加宽的做法,褶皱之后的窗帘更能彰显其飘逸、灵动的效果.其中,窗宽度的1.5倍为平褶皱,窗宽度的2倍为波浪褶皱.如图②,小莉房间的窗户呈长方形,窗户的宽度(AD)比高度(AB)的少0.5m,某种窗帘的价格为120元/m2.如果以波浪褶皱的方式制作该种窗帘比以平褶皱的方式费用多180元,求小莉房间窗户的宽度与高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形.
(1)如图(1),点E在线段AB上,点D在射线CB上,且ED=EC.将△BCE绕点C顺时针旋转60°至△ACF,连接EF.猜想线段AB,DB,AF之间的数量关系;
(2)点E在线段BA的延长线上,其它条件与(1)中一致,请在图(2)的基础上将图形补充完整,并猜想线段AB,DB,AF之间的数量关系;
(3)请选择(1)或(2)中的一个猜想进行证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是【A,B】的好点,但点D是【B,A】的好点.

知识运用:如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.

(1)数______所表示的点是【M,N】的好点;
(2)如图3,A、B为数轴上两点,点A所表示的数为-20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

-
科目: 来源: 题型:
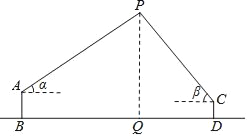
查看答案和解析>>【题目】如图,爸爸和小莉在两处观测气球的仰角分别为α、β,两人的距离(BD)是200m,如果爸爸的眼睛离地面的距离(AB)为1.6m,小莉的眼睛离地面的距离(CD)为1.2m,那么气球的高度(PQ)是多少m?(用含α、β的式子表示)
相关试题

