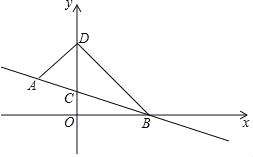
【题目】如图,在平面直角坐标系中,直线AB过点A(﹣1,1),B(2,0),交y轴于点C,点D (0,n)在点C上方.连接AD,BD.
(1)求直线AB的关系式;
(2)求△ABD的面积;(用含n的代数式表示)
(3)当S△ABD=2时,作等腰直角三角形DBP,使DB=DP,求出点P的坐标.
参考答案:
【答案】(1)y=﹣![]() x+
x+![]() ;(2)
;(2)![]() n﹣1;(3)P(2,4)或(﹣2,0).
n﹣1;(3)P(2,4)或(﹣2,0).
【解析】
(1)设直线AB的解析式为:y=kx+b,把点A(﹣1,1),B(2,0)代入即可得到结论;
(2)由(1)知:C(0,![]() ),得到CD=n﹣
),得到CD=n﹣![]() ,根据三角形的面积公式即可得到结论;
,根据三角形的面积公式即可得到结论;
(3)根据三角形的面积得到D(0,2),求得OD=OB,推出△BOD三等腰直角三角形,根据勾股定理得到BD=2![]() ,根据等腰直角三角形的性质即可得到结论.
,根据等腰直角三角形的性质即可得到结论.
解:(1)设直线AB的解析式为:y=kx+b,
把点A(﹣1,1),B(2,0)代入得,![]() ,
,
解得: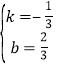 ,
,
∴直线AB的关系式为:y=﹣![]() x+
x+![]() ;
;
(2)由(1)知:C(0,![]() ),
),
∴CD=n﹣![]() ,
,
∴△ABD的面积=![]() ×(n﹣
×(n﹣![]() )×1+
)×1+![]() (n﹣
(n﹣![]() )×2=
)×2=![]() n﹣1;
n﹣1;
(3)∵△ABD的面积=![]() n﹣1=2,
n﹣1=2,
∴n=2,
∴D(0,2),
∴OD=OB,
∴△BOD三等腰直角三角形,
∴BD=2![]() ,
,
如图,∵△DBP是等腰直角三角形,DB=DP,
∴∠DBP=45°,
∴∠OBD=45°,
∴∠OBP=90°,
∴PB=![]() DB=4,
DB=4,
∴P(2,4)或(﹣2,0).
故答案为:(1)y=﹣![]() x+
x+![]() ;(2)
;(2)![]() n﹣1;(3)P(2,4)或(﹣2,0).
n﹣1;(3)P(2,4)或(﹣2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解不等式
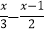 ≤1,并把它的解集在数轴上表示出来;
≤1,并把它的解集在数轴上表示出来;(2)若关于x的一元一次不等式x≥a只有3个负整数解,则a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】QQ运动记录的小莉爸爸2017年2月份7天步行的步数(单位:万步)如下表:
日期
2月6日
2月7日
2月8日
2月9日
2月10日
2月11日
2月12日
步数
2.1
1.7
1.8
1.9
2.0
1.8
2.0
(1)制作适当的统计图表示小莉爸爸这7天步行的步数的变化趋势;
(2)求小莉爸爸这7天中每天步行的平均步数;
(3)估计小莉爸爸2月份步行的总步数.
-
科目: 来源: 题型:
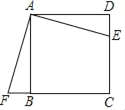
查看答案和解析>>【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)求证:△ADE≌△ABF.
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,窗帘的褶皱是指按照窗户的实际宽度将窗帘布料以一定比例加宽的做法,褶皱之后的窗帘更能彰显其飘逸、灵动的效果.其中,窗宽度的1.5倍为平褶皱,窗宽度的2倍为波浪褶皱.如图②,小莉房间的窗户呈长方形,窗户的宽度(AD)比高度(AB)的少0.5m,某种窗帘的价格为120元/m2.如果以波浪褶皱的方式制作该种窗帘比以平褶皱的方式费用多180元,求小莉房间窗户的宽度与高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上A、B两点分别对应有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|,利用数形结合思想回答下列问题:

(1)数轴上表示2和10两点之间的距离是____,数轴上表示2和-10两点之间的距离是____;
(2)数轴上,x和-2两点之间的距离是|x+2|_____;
(3)若x表示一个有理数,则|x-1+|x+2|有最小值吗?若有,请求出最小值,若没有,写出理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形.
(1)如图(1),点E在线段AB上,点D在射线CB上,且ED=EC.将△BCE绕点C顺时针旋转60°至△ACF,连接EF.猜想线段AB,DB,AF之间的数量关系;
(2)点E在线段BA的延长线上,其它条件与(1)中一致,请在图(2)的基础上将图形补充完整,并猜想线段AB,DB,AF之间的数量关系;
(3)请选择(1)或(2)中的一个猜想进行证明.

相关试题

