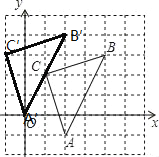
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)写出点A、B的坐标:
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,画出△A′B′C′;
(3)若AB边上有一点M(a,b),平移后对应的点M′的坐标为:
(4)求△ABC的面积.

参考答案:
【答案】(1)A(2,-1),B(4,3);(2)见解析;(3)M′(a-2,b+1);(4)5.
【解析】试题分析:(1)、根据平面直角坐标系得出点A和点B的坐标;(2)、根据图像的平移法则首先得出平移后的点的位置,然后进行顺次连接得出图像;(3)、根据平移法则得到点的坐标;(4)、利用矩形的面积减去三个直角三角形的面积得出△ABC的面积.
试题解析:(1)、A(2,-1);B(4,3);
(2)、如图所示:
(3)、M′(a-2,b+1);
(4)、S=3×4-1×3÷2-2×4÷2-1×3÷2=12-1.5-4-1.5=5.
-
科目: 来源: 题型:
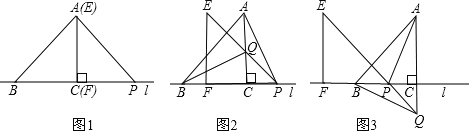
查看答案和解析>>【题目】如图,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线 l上,边EF与边AC重合,且EF=FP.
(1)在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连结AP,
BQ.猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想;
(3)AP,BQ .你认为(2)中所猜想的BQ 与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E、B、F、C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )

A. AB=DE B. DF∥AC C. ∠E=∠ABC D. AB∥DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12cm2吗? 若能,求出两段铁丝的长度;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解2018届本科生的就业情况,某网站对2018届本科生的签约状况进行了网络调查,至4月底,参与网络调查的12000人中,只有4320人已与用人单位签约在这个调查中,样本容量是__________.
-
科目: 来源: 题型:
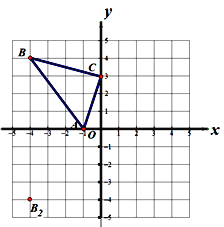
查看答案和解析>>【题目】如图所示,在直角坐标系xOy中,△ABC三点的坐标分别为A(-l,0),B(-4,4),C(0,3).
(1)在图中画出△ABC关于y轴对称的图形△A1B1C1;写出B1的坐标为___________.
(2)填空:在图中,若B2(-4,-4)与点B关于一条直线成轴对称,则这条对称轴是________,此时点C关于这条直线的对称点C2的坐标为_____________;
(3)在y轴上确定一点P,使△APB的周长最小.(注:简要说明作法,保留作图痕迹,不求坐标)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )

A. 24m B. 25m C. 28m D. 30m
相关试题

