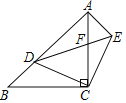
【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE.下列结论:①△ACE≌△BCD;②若∠BCD=25°,则∠AED=65°;③DE2=2CFCA;④若AB=3![]() ,AD=2BD,则AF=
,AD=2BD,则AF=![]() .其中正确的结论是______.(填写所有正确结论的序号)
.其中正确的结论是______.(填写所有正确结论的序号)
参考答案:
【答案】①②③
【解析】
先判断出∠BCD=∠ACE,即可判断出①正确;
先求出∠BDC=110°,进而得出∠AEC=110°,即可判断出②正确;
先判断出∠CAE=∠CEF,进而得出△CEF∽△CAE,即可得出CE2=CFAC,最后用勾股定理即可得出③正确;
先求出BC=AC=3,再求出BD=![]() ,进而求出CE=CD=
,进而求出CE=CD=![]() ,求出CF=
,求出CF=![]() ,即可判断出④错误.
,即可判断出④错误.
∵∠ACB=90°,
由旋转知,CD=CE,∠DCE=90°=∠ACB,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
 ,
,
∴△BCD≌△ACE,故①正确;
∵∠ACB=90°,BC=AC,
∴∠B=45°
∵∠BCD=25°,
∴∠BDC=180°-45°-25°=110°,
∵△BCD≌△ACE,
∴∠AEC=∠BDC=110°,
∵∠DCE=90°,CD=CE,
∴∠CED=45°,
则∠AED=∠AEC-∠CED=65°,故②正确;
∵△BCD≌△ACE,
∴∠CAE=∠CBD=45°=∠CEF,
∵∠ECF=∠ACE,
∴△CEF∽△CAE,
∴![]() ,
,
∴CE2=CFAC,
在等腰直角三角形CDE中,DE2=2CE2=2CFAC,故③正确;
如图,过点D作DG⊥BC于G,
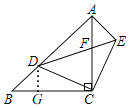
∵AB=3![]() ,
,
∴AC=BC=3,
∵AD=2BD,
∴BD=![]() AB=
AB=![]() ,
,
∴DG=BG=1,
∴CG=BC-BG=3-1=2,
在Rt△CDG中,根据勾股定理得,CD=![]() ,
,
∵△BCD≌△ACE,
∴CE=![]() ,
,
∵CE2=CFAC,
∴CF=![]() ,
,
∴AF=AC-CF=3-![]() =
=![]() ,故④错误,
,故④错误,
故答案为:①②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l1:y=﹣
 x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
A.
 B.
B.  C.
C.  D. 2
D. 2
-
科目: 来源: 题型:
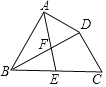
查看答案和解析>>【题目】如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )
A.
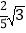 B.
B. 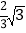 C.
C. 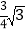 D.
D. 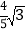
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=AD,连接BD,点E在AB上,且∠BDE=15°,DE=4
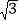 ,DC=2
,DC=2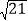 .
.(1)求BE的长;
(2)求四边形DEBC的面积.
(注意:本题中的计算过程和结果均保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】边长为
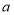 ,
,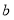 的矩形发生形变后成为边长为
的矩形发生形变后成为边长为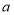 ,
,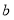 的平行四边形,如图1,平行四边形
的平行四边形,如图1,平行四边形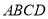 中,
中,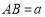 ,
,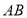 边上的高为
边上的高为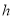 ,我们把
,我们把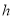 与
与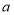 的比值叫做这个平行四边形的“形变比”.
的比值叫做这个平行四边形的“形变比”.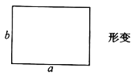
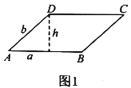
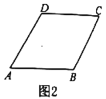
(1)若形变后是菱形
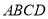 (如图2),则形变前是什么图形?
(如图2),则形变前是什么图形?(2)若图2中菱形
 的“形变比”为
的“形变比”为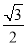 ,求菱形
,求菱形 形变前后的面积之比;
形变前后的面积之比;(3)当边长为3,4的矩形变后成为一个内角是30°的平行四边形时,求这个平行四边形的“形变比”.
相关试题

