搜索
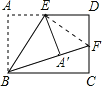
【题目】如图，矩形ABCD中，AB=1，E、F分别为AD、CD的中点，沿BE将△ABE折叠，若点A恰好落在BF上，则AD= ．
参考答案：
【答案】
．
【解析】
试题分析：连接EF，则可证明△EA′F≌△EDF，从而根据BF=BA′+A′F，得出BF的长，在Rt△BCF中，利用勾股定理可求出BC，即得AD的长度．
解：连接EF，
∵点E、点F是AD、DC的中点，
∴AE=ED，CF=DF=
CD=AB=，
由折叠的性质可得AE=A′E，
∴A′E=DE，
在Rt△EA′F和Rt△EDF中，
∵
，
∴Rt△EA′F≌Rt△EDF（HL），
∴A′F=DF=
，
∴BF=BA′+A′F=AB+DF=1+=
，
在Rt△BCF中，BC=
=．
∴AD=BC=．
故答案为：．
-
科目： 来源： 题型：
查看答案和解析>>【题目】定理“等腰三角形的两个底角相等”的逆定理是：_________________________________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=
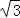x2的图象如图，点O为坐标原点，点A在y轴的正半轴上，点B、C在二次函数y=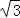x2的图象上，四边形OBAC为菱形，且∠OBA=120°，则菱形OBAC的面积为 ．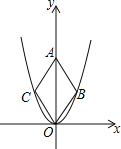
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知D是△ABC的边BC所在直线上的一点，与B，C不重合，过D分别作DF∥AC交AB所在直接于F，DE∥AB交AC所在直线于E．若∠A=80°，则∠FDE的度数是__．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=﹣mx2+4x+2m与x轴交于点A（α，0），B（β，0），且
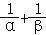=﹣2，
（1）求抛物线的解析式．
（2）抛物线的对称轴为l，与y轴的交点为C，顶点为D，点C关于l的对称点为E，是否存在x轴上的点M，y轴上的点N，使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．
（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形时，求点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在矩形AOBC中，OB=6，OA=4，分别以OB，OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系．F是边BC上一点（不与B、C两点重合），过点F的反比例函数y=
（k＞0）图象与AC边交于点E．
（1）请用k的表示点E，F的坐标；
（2）若△OEF的面积为9，求反比例函数的解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下列填空．如右图,已知AD⊥BC,EF⊥BC,∠1=∠2. 求证: DG∥BA.
证明：∵AD⊥BC,EF⊥BC（已知）
∴∠EFB=∠ADB=90° ( )
∴ ∥ ( )
∴∠1=∠BAD ( )
又∵∠1=∠2 （已知）
∴ （等量代换）
∴DG∥BA. ( )
相关试题
