【题目】如图四边形ABCD是实验中学的一块空地的平面图,其中∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m现计划在空地上植上草地绿化环境,若每平方米的草皮需150元;问需投入资金多少元? 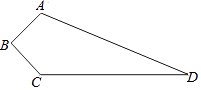
参考答案:
【答案】解:连接AC, 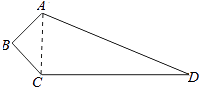
在Rt△ABC中,AC2=AB2+BC2=32+42=52 ,
∴AC=5.
在△DAC中,CD2=122 , AD2=132 ,
而122+52=132 ,
即AC2+CD2=AD2 ,
∴∠DCA=90°,
S四边形ABCD=S△BAC+S△DAC= ![]() BCAB+
BCAB+ ![]() DCAC,
DCAC,
= ![]() ×4×3+
×4×3+ ![]() ×12×5=36(m2);
×12×5=36(m2);
36×150=5400(元),.
答:总共需要投入5400元.
【解析】连接AC,在直角三角形ABC中可求得AC的长,由AC、AD、DC的长度关系可得△DAC为一直角三角形,DA为斜边;由此看,四边形ABCD由Rt△ABC和Rt△DAC构成,则容易求出面积,面积乘以单价即可得出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2﹣6x﹣5=0两根为a、b,则
①a+b=
②ab= . -
科目: 来源: 题型:
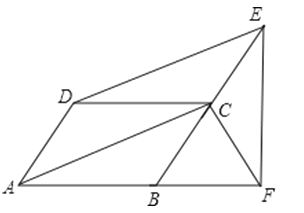
查看答案和解析>>【题目】已知:如图,四边形ABCD是平行四边形,DE∥AC,交BC的延长线于点E,EF⊥AB于点F,求证:AD=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图一,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=x-2经过A、C两点,且AB=2.
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设s=
 ,当t为何值时,s有最小值,并求出最小值.
,当t为何值时,s有最小值,并求出最小值.(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若(3x+a)(x﹣2)的乘积中不含x一次项,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x为何值时,代数式x2-13x+12的值与代数式-4x2+18的值相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-2x+k=0.
(1)若方程有实数根,求k的取值范围;
(2)如果k是满足条件的最大的整数,且方程x2-2x+k=0一根的相反数是一元二次方程(m-1)x2-3mx-7=0的一个根,求m的值及这个方程的另一根.
相关试题

