【题目】已知:如图,四边形ABCD是平行四边形,DE∥AC,交BC的延长线于点E,EF⊥AB于点F,求证:AD=CF.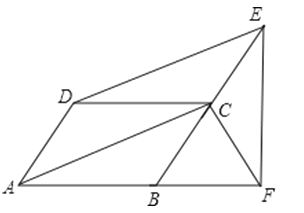
参考答案:
【答案】证明:∵DE∥AC,
∴∠DEC=∠ACB,∠EDC=∠DCA,
∵四边形ABCD是平行四边形,
∴∠CAB=∠DCA,
∴∠EDC=∠CAB,
又∵AB=CD,
∴△EDC≌△CAB,
∴CE=CB,
所以在Rt△BEF中,FC为其中线,
所以FC=BC,
即FC=AD.
【解析】利用平行四边形及平行线证明△EDC≌△CAB,可得BC=CE,即FC为直角三角形的中线,由直角三角形的性质即可得出结论.
【考点精析】掌握平行四边形的性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:(2x+3)2-25=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程s(km)与北京时间t(时)的函数图象如图所示.根据图象得到下列结论,其中错误的是( )
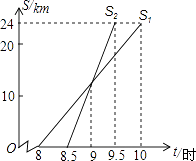
A.小亮骑自行车的平均速度是10km/h
B.妈妈比小亮提前0.5小时到达姥姥家
C.妈妈在距家12km处追上小亮
D.9:00妈妈追上小亮 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2﹣6x﹣5=0两根为a、b,则
①a+b=
②ab= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图一,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=x-2经过A、C两点,且AB=2.
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设s=
 ,当t为何值时,s有最小值,并求出最小值.
,当t为何值时,s有最小值,并求出最小值.(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
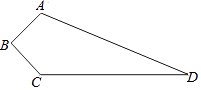
查看答案和解析>>【题目】如图四边形ABCD是实验中学的一块空地的平面图,其中∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m现计划在空地上植上草地绿化环境,若每平方米的草皮需150元;问需投入资金多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(3x+a)(x﹣2)的乘积中不含x一次项,则a= .
相关试题

