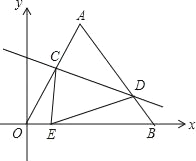
【题目】如图平面直角坐标系中,O(0,0),A(4,4![]() ),B(8,0).将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(8,0).将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=![]() ,则CE:DE的值是 .
,则CE:DE的值是 .
参考答案:
【答案】![]() .
.
【解析】如图,过A作AF⊥OB于F,
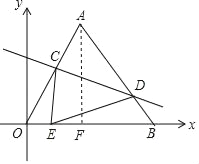
∵A(4,4![]() ),B(8,0),
),B(8,0),
∴AF=4![]() ,OF=4,OB=8,
,OF=4,OB=8,
∴BF=8﹣4=4,
∴OF=BF,
∴AO=AB,
∵tan∠AOB=![]() =
=![]() ,
,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴∠AOB=∠ABO=60°,
∵将△OAB沿直线线CD折叠,使点A恰好落在线段OB上的点E处,
∴∠CED=∠OAB=60°,
∴∠OCE=∠DEB,
∴△CEO∽△DBE,
∴![]() ,
,
设CE=a,则CA=a,CO=8﹣a,ED=b,则AD=b,DB=8﹣b,
∴![]() ,
,
∴32b=88a﹣11ab ①,
![]() ,
,
∴56a=88b﹣11ab ②,
②﹣①得:56a﹣32b=88b﹣88a,
∴![]() ,
,
即CE:DE=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠AOE=2∠EOC.
(1)若∠AOD=75°,求∠AOE的度数.
(2)若∠DOE=36°,求∠EOC的度数.

-
科目: 来源: 题型:
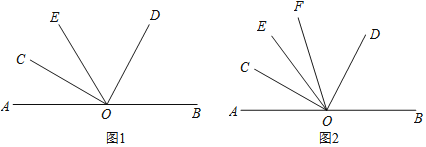
查看答案和解析>>【题目】点O为直线AB上一点,在直线AB上侧任作一个∠COD,使∠COD=90°.
(1)如图1,过点O作射线OE,使OE是∠AOD的角平分线,求证:∠BOD=2∠COE;
(2)如图2,过点O作射线OE,使OC是∠AOE的角平分线,另作射线OF,使OF是∠COD的平分线,若∠EOC=3∠EOF,求∠AOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
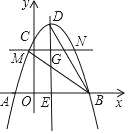
如图,抛物线y=﹣
 x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,其对称轴与抛物线交于点D.与x轴交于点E.
x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,其对称轴与抛物线交于点D.与x轴交于点E.(1)求点A,B,D的坐标;
(2)点G为抛物线对称轴上的一个动点,从点D出发,沿直线DE以每秒2个单位长度的速度运动,过点C作x轴的平行线交抛物线于M,N两点(点M在点N的左边).
设点G的运动时间为ts.
①当t为何值时,以点M,N,B,E为顶点的四边形是平行四边形;
②连接BM,在点G运动的过程中,是否存在点M.使得∠MBD=∠EDB,若存在,求出点M的坐标;若不存在,请说明理由;
(3)点Q为坐标平面内一点,以线段MN为对角线作萎形MENQ,当菱形MENQ为正方形时,请直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、B、C是直线l上的三个点,线段AB=8厘米.
(1)若AB=2BC,求线段AC的长度;
(2)若点C是线段AB的中点,点P、Q是直线l上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、B同时出发在直线上运动,则经过多少秒时线段PQ的长为5厘来?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 城气象台测得台风中心在
城气象台测得台风中心在 城正西方向
城正西方向 的
的 处,以每小时
处,以每小时 的速度向南偏东
的速度向南偏东 的
的 方向移动,距台风中心
方向移动,距台风中心 的范围内是受台风影响的区域.
的范围内是受台风影响的区域.
(1)求
 城与台风中心之间的最小距离;(2)求
城与台风中心之间的最小距离;(2)求 城受台风影响的时间有多长?
城受台风影响的时间有多长? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.

相关试题

