【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠AOE=2∠EOC.
(1)若∠AOD=75°,求∠AOE的度数.
(2)若∠DOE=36°,求∠EOC的度数.

参考答案:
【答案】(1)40°;(2)18°
【解析】
(1)由∠AOC与∠BOC互余可得∠AOC+∠BOC=90°,根据角的和差关系可得∠BOD=15°,再根据角平分线的定义可得∠BOC=30°,从而得出∠AOC的度数,然后根据∠AOE=2∠EOC即可求出∠AOE的度数;
(2)设∠EOC=x,则∠AOE=2x,根据题意列方程求解即可.
解:(1)∵∠AOC与∠BOC互余,
∴∠AOC+∠BOC=90°,
即∠AOB=90°,
∵∠AOD=75°,
∴∠BOD=15°,
又∵OD平分∠BOC,
∴∠BOC=30°,
∴∠AOC=60°,
又∵∠AOE=2∠EOC,
∴![]() ;
;
(2)∠EOC=x,则
∠DOC=∠DOE﹣∠EOC=36°﹣x,
∵OD平分∠BOC,
∴∠BOC=2∠DOC=2(36°﹣x),
又∵∠AOE=2∠EOC,
∴∠AOE=2x,
∴2x+x+2(36°﹣x)=90°,
∴x=18°.
即∠EOC=18°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从
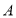 城出发匀速行驶至
城出发匀速行驶至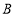 城在个行驶过程中甲乙两车离开
城在个行驶过程中甲乙两车离开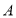 城的距离
城的距离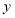 (单位:千米)与甲车行驶的时间
(单位:千米)与甲车行驶的时间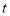 (单位:小时)之间的函数关系如图所示.则下列结论: ①
(单位:小时)之间的函数关系如图所示.则下列结论: ①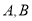 两城相距
两城相距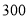 千米;②乙车比甲车晚出发
千米;②乙车比甲车晚出发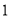 小时,却早到
小时,却早到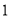 小时;③乙车出发后
小时;③乙车出发后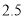 小时追上甲车;④在乙车行驶过程中.当甲、乙两车相距
小时追上甲车;④在乙车行驶过程中.当甲、乙两车相距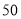 千米时,
千米时, 或
或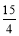 ,其中正确的结论是_________.
,其中正确的结论是_________.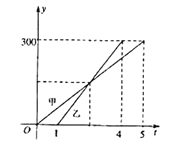
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
问题背景
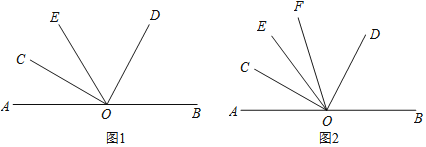
折纸是一种许多人熟悉的活动,将折纸的一边二等分、四等分都是比较容易做到的,但将一边三等分就不是那么容易了,近些年,经过人们的不懈努力,已经找到了多种将正方形折纸一边三等分的精确折法,最著名的是由日本学者芳贺和夫发现的三种折法,现在被数学界称之为芳贺折纸三定理.其中,芳贺折纸第一定理的操作过程及内容如下(如图1):
操作1:將正方形ABCD对折,使点A与点D重合,点B与点C重合.再将正方形ABCD展开,得到折痕EF;
操作2:再将正方形纸片的右下角向上翻折,使点C与点E重合,边BC翻折至B'E的位置,得到折痕MN,B'E与AB交于点P.则P即为AB的三等分点,即AP:PB=2:1.

解决问题
(1)在图1中,若EF与MN交于点Q,连接CQ.求证:四边形EQCM是菱形;
(2)请在图1中证明AP:PB=2:l.
发现感悟
若E为正方形纸片ABCD的边AD上的任意一点,重复“问题背景”中操作2的折纸过程,请你思考并解决如下问题:
(3)如图2.若
 =2.则
=2.则 = ;
= ;(4)如图3,若
 =3,则
=3,则 = ;
= ;(5)根据问题(2),(3),(4)给你的启示,你能发现一个更加一般化的结论吗?请把你的结论写出来,不要求证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商场采购员要到厂家批发购买篮球和排球共
 个,篮球个数不少于排球个数,付款总额不得超过
个,篮球个数不少于排球个数,付款总额不得超过 元,已知两种球厂的批发价和商场的零售价如下表. 设该商场采购
元,已知两种球厂的批发价和商场的零售价如下表. 设该商场采购 个篮球.
个篮球.品名
厂家批发价/元/个
商场零售价/元/个
篮球


排球


(1)求该商场采购费用
 (单位:元)与
(单位:元)与 (单位:个)的函数关系式,并写出自变最
(单位:个)的函数关系式,并写出自变最 的取值范围:
的取值范围:(2)该商场把这
 个球全都以零售价售出,求商场能获得的最大利润;
个球全都以零售价售出,求商场能获得的最大利润;(3)受原材料和工艺调整等因素影响,采购员实际采购时,低球的批发价上调了
 元/个,同时排球批发价下调了
元/个,同时排球批发价下调了 元/个.该体有用品商场决定不调整商场零售价,发现将
元/个.该体有用品商场决定不调整商场零售价,发现将 个球全部卖出获得的最低利润是
个球全部卖出获得的最低利润是 元,求
元,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】点O为直线AB上一点,在直线AB上侧任作一个∠COD,使∠COD=90°.
(1)如图1,过点O作射线OE,使OE是∠AOD的角平分线,求证:∠BOD=2∠COE;
(2)如图2,过点O作射线OE,使OC是∠AOE的角平分线,另作射线OF,使OF是∠COD的平分线,若∠EOC=3∠EOF,求∠AOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
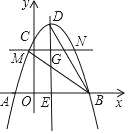
如图,抛物线y=﹣
 x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,其对称轴与抛物线交于点D.与x轴交于点E.
x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,其对称轴与抛物线交于点D.与x轴交于点E.(1)求点A,B,D的坐标;
(2)点G为抛物线对称轴上的一个动点,从点D出发,沿直线DE以每秒2个单位长度的速度运动,过点C作x轴的平行线交抛物线于M,N两点(点M在点N的左边).
设点G的运动时间为ts.
①当t为何值时,以点M,N,B,E为顶点的四边形是平行四边形;
②连接BM,在点G运动的过程中,是否存在点M.使得∠MBD=∠EDB,若存在,求出点M的坐标;若不存在,请说明理由;
(3)点Q为坐标平面内一点,以线段MN为对角线作萎形MENQ,当菱形MENQ为正方形时,请直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图平面直角坐标系中,O(0,0),A(4,4
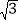 ),B(8,0).将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(8,0).将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=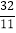 ,则CE:DE的值是 .
,则CE:DE的值是 .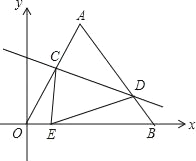
相关试题

