【题目】如图,已知点A、B、C是直线l上的三个点,线段AB=8厘米.
(1)若AB=2BC,求线段AC的长度;
(2)若点C是线段AB的中点,点P、Q是直线l上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、B同时出发在直线上运动,则经过多少秒时线段PQ的长为5厘来?
![]()
参考答案:
【答案】(1)12厘米;(2),经过![]() 或1或3秒或9秒时线段PQ的长为5厘米
或1或3秒或9秒时线段PQ的长为5厘米
【解析】
(1)根据线段的和差倍分即可得到结论;
(2)由于BC=4厘米,点P、Q分别从点C、点B同时出发在直线上运动,当线段PQ的长为5厘米时,可分四种情况进行讨论:点P向左、点Q向右运动;点P、Q都向右运动;点P、Q都向左运动;点P向右、点Q向左运动;都可以根据线段PQ的长为5厘米列出方程,解方程即可.
解:(1)点C在点B的左侧,如图1,

∵AB=8厘米,AB=2BC,
∴BC=4厘米,
∴AC=AB﹣BC=8﹣4=4厘米;
点C在点B的右侧,如图2,
![]()
∵AB=8厘米,AB=2BC,
∴BC=4厘米,
∴AC=AB+BC=8+4=12厘米;
(2)∵点C是线段AB的中点,
∴BC=4厘米,
设运动时间为t秒,PQ=5厘米.
①如果点P向左、点Q向右运动时,如图3,
![]()
由题意,得:t+2t=5﹣4,
解得t=![]() ;
;
②点P、Q都向右运动时,如图4,

由题意,得:2t﹣t=5﹣4,
解得t=1;
③点P向右、点Q向左运动,如图5,
![]()
由题意,得:2t﹣4+t=5,
解得t=3;
④点P、Q都向左运动,如图6

由题意,得:2t﹣t=5+4,
解得t=9.
综上所述,经过![]() 或1或3秒或9秒时线段PQ的长为5厘米.
或1或3秒或9秒时线段PQ的长为5厘米.
-
科目: 来源: 题型:
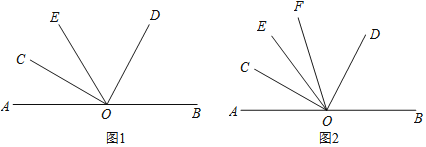
查看答案和解析>>【题目】点O为直线AB上一点,在直线AB上侧任作一个∠COD,使∠COD=90°.
(1)如图1,过点O作射线OE,使OE是∠AOD的角平分线,求证:∠BOD=2∠COE;
(2)如图2,过点O作射线OE,使OC是∠AOE的角平分线,另作射线OF,使OF是∠COD的平分线,若∠EOC=3∠EOF,求∠AOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
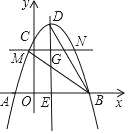
如图,抛物线y=﹣
 x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,其对称轴与抛物线交于点D.与x轴交于点E.
x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,其对称轴与抛物线交于点D.与x轴交于点E.(1)求点A,B,D的坐标;
(2)点G为抛物线对称轴上的一个动点,从点D出发,沿直线DE以每秒2个单位长度的速度运动,过点C作x轴的平行线交抛物线于M,N两点(点M在点N的左边).
设点G的运动时间为ts.
①当t为何值时,以点M,N,B,E为顶点的四边形是平行四边形;
②连接BM,在点G运动的过程中,是否存在点M.使得∠MBD=∠EDB,若存在,求出点M的坐标;若不存在,请说明理由;
(3)点Q为坐标平面内一点,以线段MN为对角线作萎形MENQ,当菱形MENQ为正方形时,请直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图平面直角坐标系中,O(0,0),A(4,4
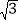 ),B(8,0).将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(8,0).将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=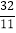 ,则CE:DE的值是 .
,则CE:DE的值是 .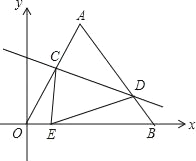
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 城气象台测得台风中心在
城气象台测得台风中心在 城正西方向
城正西方向 的
的 处,以每小时
处,以每小时 的速度向南偏东
的速度向南偏东 的
的 方向移动,距台风中心
方向移动,距台风中心 的范围内是受台风影响的区域.
的范围内是受台风影响的区域.
(1)求
 城与台风中心之间的最小距离;(2)求
城与台风中心之间的最小距离;(2)求 城受台风影响的时间有多长?
城受台风影响的时间有多长? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.

-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级全体同学参加了学校捐款活动,随机抽取了部分同学捐款的情况统计图如图所示
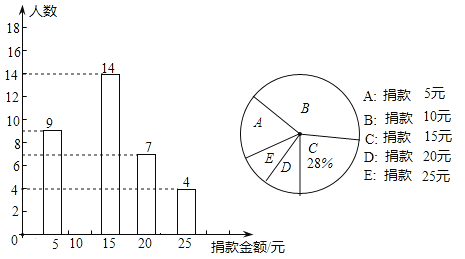
(1)本次共抽查学生 人,并将条形统计图补充完整;
(2)捐款金额的众数是 ,中位数是 ;
(3)在八年级600名学生中,捐款20元及以上的学生估计有 人.
相关试题

