【题目】如图,已知△ABC中,AB=AC,D为△ABC所在平面内的一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB于点E,F.
(1)如图1,当点D在线段BC上时,通过观察分析线段DE、DF、AB之间的数量关系,并说明理由;
(2)如图2,当点D在直线BC上,其他条件不变时,试猜想线段DE、DF、AB之间的数量关系(请直接写出等式,不需证明);
(3)如图3,当点D是△ABC内一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB和直线BC于E、F和G. 试猜想线段DE、DF、DG与AB之间的数量关系(请直接写出等式,不需证明).

参考答案:
【答案】(1)DE+DF=AB.理由见解析; (2) ①当点D在CB的延长线上时, AB=DE-DF;②当点D在线段BC上时,AB=DE+DF;③当点D在BC的延长线上时, AB=DF-DE.(3)AB=DE+DG+DF.
【解析】
(1)如图1,先根据两组对边分别平行的四边形是平行四边形得出四边形AEDF是平行四边形,则DE=AF.再根据平行线及等腰三角形的性质得出∠FDB=∠B,由等角对等边得到DF=FB,从而证明DE+DF=AF+FB=AB;
(2)当点D在直线BC上时,分三种情况:
①当点D在BC的反向延长线上时,如图4,先证明四边形AEDF是平行四边形,则DE=AF,再证明∠FDB=∠FBD,由等角对等边得到DF=FB,从而证明AB=AF-BF=DE-DF;
②当点D在线段BC上时,如图1,AB=DE+DF;
③当点D在BC的延长线上时,如图5,先证明四边形AEDF是平行四边形,则DF=AE,再证明∠CDE=∠DCE,由等角对等边得到CE=DE,再证明从而证明AB=AC=AE-CE=DF-DE;
(3)如图3,先证明四边形AEDF是平行四边形,则DF=AE,再证明∠EGC=∠C,由等角对等边得到DE+DG=CE,从而证明AB=AC=EC+AE=DE+DG+DF.
(1)DE+DF=AB. 理由如下:
如图1,∵DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
∴DE=AF.
∵DF∥AC,
∴∠FDB=∠C,
∵AB=AC,
∴∠C=∠B,
∴∠FDB=∠B,
∴DF=FB,
∴DE+DF=AF+FB=AB;
(2)
①当点D在BC的反向延长线上时,如图4,AB=DE-DF;
∵DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
∴DE=AF.
∴∠FDB=∠BCA,
∵AB=AC,
∴∠BCA =∠B,
∴∠FDB=∠B=∠DBF,
∴DF=FB,
∴AB=AF-BF=DE-DF;;
②当点D在线段BC上时,同题(1),AB=DE+DF;
③当点D在BC的延长线上时,如图5,AB=DF-DE;
∵DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
∴DF=AE.
∴∠CDE=∠B,
∵AB=AC,
∴∠BCA =∠B=∠DCE ,
∴∠CDE=∠DCE,
∴CE=DE,
∴AB=AC=AE-CE=DF-DE;;
(3)AB=DE+DG+DF.
∵DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
∴DF=AE,
∵DE∥AB,
∴∠EGC=∠B,
∵AB=AC,
∴∠C=∠B,
∴∠C=∠EGC,
∴EG=EC,即DE+DG=CE,
∴AB=AC=EC+AE=DE+DG+DF.
故答案为:(1)DE+DF=AB. 理由见解析;(2)①当点D在BC的反向延长线上时,如图4见解析,AB=DE-DF;②当点D在线段BC上时,同题(1),AB=DE+DF;③当点D在BC的延长线上时,如图5见解析,AB=DF-DE;(3)AB=DE+DG+DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三位数
 其中a、b、c不全相等且都不为
其中a、b、c不全相等且都不为 ,重新排列各数位上的数字可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为
,重新排列各数位上的数字可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为 例如,536的差数
例如,536的差数 .
.(1)
 ______,
______, ______.
______.(2)若一个三位数
 其中
其中 且都不为
且都不为 ,求证:
,求证: 能被99整除.
能被99整除.(3)若s、t是各数位上的数字均不为0且互不相等两个三位自然数,s的个位数字为1,十位数字是个位数字的3倍,百位数字为x,t的百位数字为y,十位数字是百位数字的2倍,t的个位数字与s的百位数字相同
 ,若
,若 能被3整除,
能被3整除, 能被11整除,求
能被11整除,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 ∥
∥ ,
,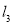 、
、 和
和 、
、 分别交于点
分别交于点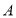 、
、 、
、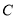 、
、 ,点
,点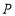 在直线
在直线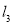 或
或 上且不与点
上且不与点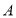 、
、 、
、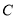 、
、 重合.记
重合.记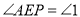 ,
,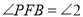 ,
,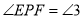 .
.(1)若点
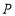 在图(1)位置时,求证:
在图(1)位置时,求证: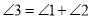 ;
;(2)若点
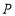 在图(2)位置时,请直接写出
在图(2)位置时,请直接写出 、
、 、
、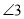 之间的关系;
之间的关系;(3)若点
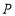 在图(3)位置时,写出
在图(3)位置时,写出 、
、 、
、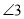 之间的关系并给予证明.
之间的关系并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A表示的有理数为
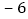 ,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度由
,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度由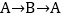 运动,同时,点Q从点B出发以每秒1个单位长度的速度由
运动,同时,点Q从点B出发以每秒1个单位长度的速度由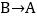 运动,当点Q到达点A时P、Q两点停止运动,设运动时间为
运动,当点Q到达点A时P、Q两点停止运动,设运动时间为 单位:秒
单位:秒 .
.(1)求
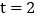 时,求点P和点Q表示的有理数;
时,求点P和点Q表示的有理数;(2)求点P与点Q第一次重合时的t值;
(3)当t的值为多少时,点P表示的有理数与点Q表示的有理数距离是3个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别为(0,3)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A'B'OC'.
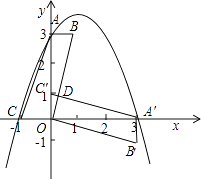
(1)若抛物线过点C,A,A',求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形A'B'OC'重叠部分△OC'D的周长;
(3)点M是第一象限内抛物线上的一动点,问:点M在何处时;△AMA'的面积最大?最大面积是多少?并求出此时M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
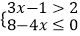 的解集在数轴上表示为( )
的解集在数轴上表示为( )
A.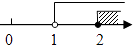
B.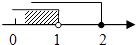
C.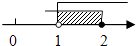
D.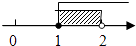
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子里,有5个除颜色外,其他都相同的小球,其中有3个是红球,2个是绿球,每次拿一个球然后放回去,拿2次,则至少有一次取到绿球的概率是 .
相关试题

