【题目】若一个三位数![]() 其中a、b、c不全相等且都不为
其中a、b、c不全相等且都不为![]() ,重新排列各数位上的数字可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为
,重新排列各数位上的数字可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为![]() 例如,536的差数
例如,536的差数![]() .
.
(1)![]() ______,
______,![]() ______.
______.
(2)若一个三位数![]() 其中
其中![]() 且都不为
且都不为![]() ,求证:
,求证:![]() 能被99整除.
能被99整除.
(3)若s、t是各数位上的数字均不为0且互不相等两个三位自然数,s的个位数字为1,十位数字是个位数字的3倍,百位数字为x,t的百位数字为y,十位数字是百位数字的2倍,t的个位数字与s的百位数字相同![]() ,若
,若![]() 能被3整除,
能被3整除,![]() 能被11整除,求
能被11整除,求![]() 的值.
的值.
参考答案:
【答案】![]() ,
,![]() ;
;![]() 见解析;
见解析;![]() .
.
【解析】
![]() 根据
根据![]() 的定义求解即可;
的定义求解即可;
![]() 先根据
先根据![]() 的定义,求出
的定义,求出![]() 关于a,b,c的代数式,即可证明它能被99整除;
关于a,b,c的代数式,即可证明它能被99整除;
![]() 先列出s,t的代数式,根据
先列出s,t的代数式,根据![]() 能被3整除,
能被3整除,![]() 能被11整除确定x,y的值,再根据
能被11整除确定x,y的值,再根据![]() 的定义求解即可
的定义求解即可
![]() ,
,![]() ,
,
故答案为:396,297
![]() 且都不为0,
且都不为0,
![]() ,
,
![]() 能被99整除.
能被99整除.
![]() 由题意,
由题意,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() 能被3整除,
能被3整除,
![]() ,4,7
,4,7
![]() 当
当![]() 时,
时,![]() ,
,
![]() 、t是各数位上的数字均不为0且互不相等,
、t是各数位上的数字均不为0且互不相等,
![]() 不符合题意,舍去
不符合题意,舍去
![]() 当
当![]() 时,
时,![]()
![]() ,
,![]() 能被11整除,
能被11整除,
![]() ,即
,即![]() ,
,
![]() 、t是各数位上的数字均不为0且互不相等,
、t是各数位上的数字均不为0且互不相等,
![]() 不符合题意,舍去
不符合题意,舍去
![]() 当
当![]() 时,
时,![]()
![]() ,
,![]() 能被11整除,
能被11整除,
![]() ,即
,即![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:在平面直角坐标系
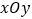 中,对于任意两点
中,对于任意两点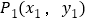 与
与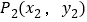 的“非常距离”,给出如下定义:
的“非常距离”,给出如下定义:若
 ,则点
,则点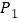 与点
与点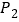 的“非常距离”为
的“非常距离”为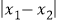 ;
;若
 ,则点
,则点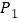 与点
与点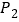 的“非常距离”为
的“非常距离”为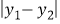 .
.例如:点
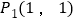 ,点
,点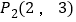 ,因为
,因为 ,所以点
,所以点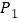 与点
与点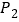 的“非常距离”为
的“非常距离”为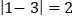 ,也就是图1中线段
,也就是图1中线段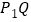 与线段
与线段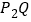 长度的较大值(点
长度的较大值(点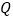 为垂直于
为垂直于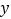 轴的直线
轴的直线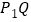 与垂直于
与垂直于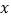 轴的直线
轴的直线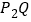 的交点).
的交点).(1)已知点
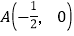 ,
,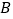 为
为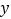 轴上的一个动点.
轴上的一个动点.①若点
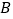 (0,3),则点
(0,3),则点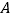 与点
与点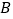 的“非常距离”为 ;
的“非常距离”为 ;②若点
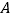 与点
与点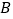 的“非常距离”为2,则点
的“非常距离”为2,则点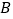 的坐标为 ;
的坐标为 ;③直接写出点
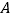 与点
与点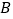 的“非常距离”的最小值为 ;
的“非常距离”的最小值为 ;(2)已知点
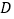 (0,1),点
(0,1),点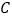 是直线
是直线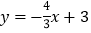 上的一个动点,如图2,求点
上的一个动点,如图2,求点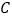 与点
与点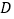 “非常距离”的最小值及相应的点
“非常距离”的最小值及相应的点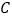 的坐标.
的坐标.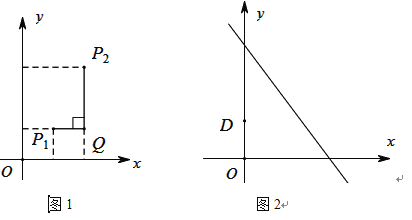
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,DE垂直平分AB,分别交AB,BC于点D,E,MN垂直平分AC,分别交AC,BC于点M,N.
(1)如图①,若∠BAC = 110°,求∠EAN的度数;
(2)如图②,若∠BAC =80°,求∠EAN的度数;
(3)若∠BAC = α(α ≠ 90°),直接写出用α表示∠EAN大小的代数式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 ∥
∥ ,
,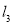 、
、 和
和 、
、 分别交于点
分别交于点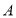 、
、 、
、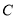 、
、 ,点
,点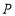 在直线
在直线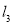 或
或 上且不与点
上且不与点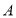 、
、 、
、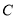 、
、 重合.记
重合.记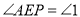 ,
,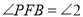 ,
,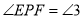 .
.(1)若点
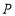 在图(1)位置时,求证:
在图(1)位置时,求证: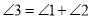 ;
;(2)若点
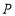 在图(2)位置时,请直接写出
在图(2)位置时,请直接写出 、
、 、
、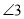 之间的关系;
之间的关系;(3)若点
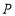 在图(3)位置时,写出
在图(3)位置时,写出 、
、 、
、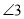 之间的关系并给予证明.
之间的关系并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A表示的有理数为
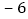 ,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度由
,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度由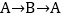 运动,同时,点Q从点B出发以每秒1个单位长度的速度由
运动,同时,点Q从点B出发以每秒1个单位长度的速度由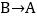 运动,当点Q到达点A时P、Q两点停止运动,设运动时间为
运动,当点Q到达点A时P、Q两点停止运动,设运动时间为 单位:秒
单位:秒 .
.(1)求
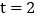 时,求点P和点Q表示的有理数;
时,求点P和点Q表示的有理数;(2)求点P与点Q第一次重合时的t值;
(3)当t的值为多少时,点P表示的有理数与点Q表示的有理数距离是3个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,D为△ABC所在平面内的一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB于点E,F.
(1)如图1,当点D在线段BC上时,通过观察分析线段DE、DF、AB之间的数量关系,并说明理由;
(2)如图2,当点D在直线BC上,其他条件不变时,试猜想线段DE、DF、AB之间的数量关系(请直接写出等式,不需证明);
(3)如图3,当点D是△ABC内一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB和直线BC于E、F和G. 试猜想线段DE、DF、DG与AB之间的数量关系(请直接写出等式,不需证明).

相关试题

