【题目】如图①,定义:在四边形ABCD中,若AD=BC,且∠ADB+∠BCA=180°,则把四边形ABCD叫作互补等对边四边形.如图②,在等腰△ABE中,AE=BE,四边形ABCD是互补等对边四边形.试说明:∠ABD=∠BAC=![]() ∠E.
∠E.

参考答案:
【答案】证明见解析.
【解析】
已知AE=BE,根据等腰三角形的性质可得∠EAB=∠EBA.根据互补等对边四边形的定义可得AD=BC.利用SAS证明△ABD≌△BAC,根据全等三角形的性质可得∠ABD=∠BAC,∠ADB=∠BCA;根据互补等对边四边形的定义可得∠ADB+∠BCA=180°,即可求得∠ADB=∠BCA=90°.在等腰△ABE中,根据等腰三角形的性质及三角形的内角和定理可得∠EAB=∠EBA=![]() (180°-∠E)=90°-
(180°-∠E)=90°-![]() ∠E,所以∠ABD=90°-∠EAB=90°-
∠E,所以∠ABD=90°-∠EAB=90°-![]() =
=![]() ∠E,由此即可证得结论.
∠E,由此即可证得结论.
∵AE=BE,
∴∠EAB=∠EBA.
∵四边形ABCD是互补等对边四边形,
∴AD=BC.
在△ABD与△BAC中,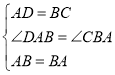 ,
,
∴△ABD≌△BAC,
∴∠ABD=∠BAC,∠ADB=∠BCA.
∵∠ADB+∠BCA=180°,
∴∠ADB=∠BCA=90°.
在等腰△ABE中,∵∠EAB=∠EBA=![]() (180°-∠E)=90°-
(180°-∠E)=90°-![]() ∠E,
∠E,
∴∠ABD=90°-∠EAB=90°-![]() =
=![]() ∠E,
∠E,
∴∠ABD=∠BAC=![]() ∠E.
∠E.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ABCD中,∠ABC为锐角,AB<BC,点E是AD上的一点,延长CE到F,连接BF交AD于点G, 使∠FBC=∠DCE.
⑴ 求证:∠D=∠F;
⑵ 在直线AD找一点P,使以点B、P、C为顶点的三角形与以点C、D、P为顶点的三角形相似.(在原图中标出准确P点的位置,必要时用直尺和圆规作出P点,保留作图的痕迹,不写作法)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在ΔABC中,DE、MN是边AB、AC的垂直平分线,其垂足分别为点D、M,分别交BC于点E、N,且DE和MN交于点F.
(1)若∠B=24°,求∠BAE的度数.
(2)若AB=8,AC=11,思考ΔAEN的周长肯定小于多少?
(3)若∠EAN=40°,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,Rt△ABC中,若AC=4,BC=3,DE⊥AC,且DE=DB,求AD的长;
(2)如图2,已知△ABC,若AB边上存在一点M,若AC边上存在一点N,使MB=MN,且△AMN∽△ABC,请利用没有刻度的直尺和圆规,作出符合条件的线段MN(注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注).
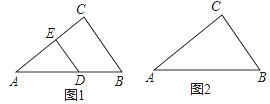
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在△ABC中,点D,E,F分别是边AB,BC,CA上的动点,若△DEF∽△ABC(点D、E、F的对应点分别为点A、B、C),则称△DEF是△ABC的子三角形,如图.
(1)已知:如图1,△ABC是等边三角形,点D,E,F分别是边AB,BC,CA上动点,且AD=BE=CF.
求证:△DEF是△ABC的子三角形.
(2)已知:如图2,△DEF是△ABC的子三角形,且AB=AC,∠A=90°,若BE=
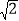 ,求CF和AD的长.
,求CF和AD的长.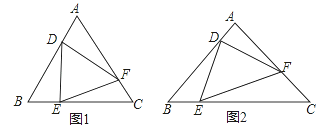
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,ΔABC中,AD⊥BC于点D,以A为直角顶点,分别以AB、AC为直角边,向ΔABC外作等腰RtΔABE和等腰RtΔACF,过点E、F作射线DA的垂线,垂足分别为Q、P.
(1)试探究线段EQ和FP之间的数量关系,并说明理由.
(2)如图②,若连接EF交DA的延长线于点H,由(1)中的结论你能判断EH与FH的大小关系吗?并说明理由.
(3)图②中的ΔABC与ΔAEF的面积相等吗?(直接给出结论,不需要说理)


-
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数y=﹣2x+1,下列结论正确的是( )
A. 图象必经过点(﹣2,1) B. 图象经过第一、二、三象限
C. 当x>
 时,y<0 D. y随x的增大而增大
时,y<0 D. y随x的增大而增大
相关试题

