Question

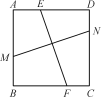
【题目】如图，正方形ABCD内有两条相交线段MN，EF，M，N，E，F分别在边AB，CD，AD，BC上．小明认为：若MN＝EF，则MN⊥EF；小亮认为：若MN⊥EF，则MN＝EF.你认为( )

A. 仅小明对 B. 仅小亮对 C. 两人都对 D. 两人都不对

Answer 1

【答案】C

【解析】

分别过点E作EG⊥BC于点G，过点M作MP⊥CD于点P，设EF与MN相交于点O，MP与EF相交于点Q，根据正方形的性质可得EG=MP；对于小明的说法，先利用“HL”证明Rt△EFG≌Rt△MNP，根据全等三角形对应角相等可得∠MNP=∠EFG，再根据角的关系推出∠EQM=∠MNP，然后根据∠MNP+∠NMP=90°得到∠NMP+∠EQM=90°，从而得到∠MOQ=90°，根据垂直的定义即可证得MN⊥EF；对于小亮的说法，先推出∠EQM=∠EFG，∠EQM=∠MNP，然后得到∠EFG=∠MNP，然后利用“角角边”证明△EFG≌△MNP，根据全等三角形对应边相等可得EF=MN．

如图，过点E作EG⊥BC于点G，过点M作MP⊥CD于点P，设EF与MN相交于点O，MP与EF相交于点Q，

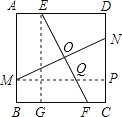
∵四边形ABCD是正方形，

∴EG=MP，

对于小明的说法：

在Rt△EFG和Rt△MNP中，

，

∴Rt△EFG≌Rt△MNP（HL），

∴∠MNP=∠EFG，

∵MP⊥CD，∠C=90°，

∴MP∥BC，

∴∠EQM=∠EFG=∠MNP，

又∵∠MNP+∠NMP=90°，

∴∠EQM+∠NMP=90°，

在△MOQ中，∠MOQ=180°-（∠EQM+∠NMP）=180°-90°=90°，

∴MN⊥EF，

故甲正确．

对小亮的说法：

∵MP⊥CD，∠C=90°，

∴MP∥BC，

∴∠EQM=∠EFG，

∵MN⊥EF，

∴∠NMP+∠EQM=90°，

又∵MP⊥CD，

∴∠NMP+∠MNP=90°，

∴∠EQM=∠MNP，

∴∠EFG=∠MNP，

在△EFG和△MNP中，

，

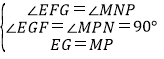∴△EFG≌△MNP（AAS），

∴MN=EF，故小亮的说法正确，

综上所述，两个人的说法都正确．

故选C．