Question

【题目】在平面直角坐标系中，已知反比例函数y=的图象经过点A，点O是坐标原点，OA=2且OA与x轴的夹角是60°．

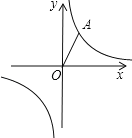
（1）试确定此反比例函数的解析式；

（2）将线段OA绕O点顺时针旋转30°得到线段OB，判断点B是否在此反比例函数的图象上，并说明理由．

Answer 1

【答案】（1）y=；（2）点B（，1）在反比例函数y=的图象上．

【解析】

试题分析：（1）作AC⊥x轴于点C，在Rt△AOC中，解直角三角形求得A点坐标为（1，），把A（1，）分别代入代入y=，根据待定系数法即可求得；

（2）作BD⊥x轴于点D，在Rt△BOD中，解直角三角形求得B点坐标为（，1），把x=代入代入y=，即可判断．

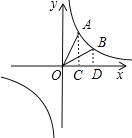
解：（1）作AC⊥x轴于点C，如图，

在Rt△AOC中，

∵OA=2，∠AOC=60°，

∴∠OAC=30°，

∴OC=OA=1，AC=OC=，

∴A点坐标为（1，），

把A（1，）代入y=，

得k=1×=，

∴反比例函数的解析式为y=；

（2）点B在此反比例函数的图象上，

理由如下：过点B作x轴的垂线交x轴于点D，

∵线段OA绕O点顺时针旋转30°得到线段OB，

∴∠AOB=30°，OB=OA=2，∴∠BOD=30°，

在Rt△BOD中，BD=OB=1，OD=BD=，

∴B点坐标为（，1），

∵当x=时，y==1，

∴点B（，1）在反比例函数y=的图象上．