【题目】如图,函数y=kx+b和函数y=ax+m的图象,求下列不等式(组)的解集

(1)kx+b<0的解集是 ;
(2)ax+m≥0的解集是 ;
(3)kx+b<ax+m的解集是 ;
(4)ax+m>kx+b>0的解集是 ;
(5)0<ax+m<kx+b的解集是 。
参考答案:
【答案】(1)x<-5 ;(2)x≤2 ;(3)x<-1 ;(4) -5<x<-1;(5)-1<x<2 .
【解析】(1)观察函数图象,结合交点的坐标以及函数图象的上下关系即可得出结论;
(2)(3)(4)观察函数图象,找出函数图象与x轴交点的坐标,结合图象在x轴上下的位置关系即可得出结论.
解:(1)观察函数图象,发现:
当x<–5时,函数y=kx+b的图象在函数y=kx+b的图象的下方,
∴kx+b<0的解集是:x<–5;
(2)观察函数图象,发现:
当x≤2时,函数y=ax+m的图象在函数y=kx+b的图象的下方,
∴ax+m≥0的解集是:x≤2;
(3)观察函数图象,发现:
当x<-1时,函数y=kx+b的图象在函数y=ax+m的图象的下方,
∴kx+b<ax+m的解集为:x<-1.
答案为:x<-1.
(4)观察函数图象,发现:
当-5
∴ax+m>kx+b>0的解集为:-5
故答案为:-5
(5)观察函数图象,发现:
当-1
∴0<ax+m<kx+b的解集为:-1
“点睛”本题考查了一次函数与一元一次不等式,解题的关键是结合函数图象解集不等式,本题属于基础题,难度不大,解决该题型题目时,数形结合解决不等式(不等式组)是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天的最高气温是5℃,最低气温是﹣4℃,则这一天气温的温差是( )
A. 1℃ B. ﹣1℃ C. 9℃ D. ﹣9℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,

(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知反比例函数y=
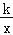 的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°.
的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°.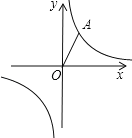
(1)试确定此反比例函数的解析式;
(2)将线段OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x+y=6,xy=5,则x2+y2=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于多项式﹣2x2+8x+5的说法正确的是( )
A. 有最大值13 B. 有最小值﹣3 C. 有最大值37 D. 有最小值1
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,以△ABC中的AB、AC为边分别向外作正方形ADEB、ACGF,
连接DC、BF。(相关知识链接:正方形的四条边都相等,四个角都是直角)
(1)观察图形,利用旋转的观点说明:
△ADC绕着点__ ___逆时针旋转___ __°得到△ABF。
(2)猜想:CD与BF有怎样的数量关系和位置关系?并证明你的猜想.
(3)若CD与BF相交于点M,求∠AMF的度数。

相关试题

