【题目】已知点A(3,4),点B为直线x=1上的动点,设B(-1,y).

(1)如图①,若△ABO是等腰三角形且AO=AB时,求点B的坐标;
(2)如图②,若点C(x,0)且-1<x<3,BC⊥AC垂足为点C;
①当x=0时,求tan∠BAC的值;
②若AB与y轴正半轴的所夹锐角为α,当点C在什么位置时tanα的值最大?
参考答案:
【答案】⑴B(-1,1)或B(-1,7)⑵①![]() ②当C(1,0)时,tanα有最大值
②当C(1,0)时,tanα有最大值![]()
【解析】试题分析:(1)在Rt△ABE中,根据勾股定理得到![]() ,得到结论;
,得到结论;
(2)①由C(x,0),当x=0时,点C与O重合,如图,设直线x=-1与x轴交于G点,过A作AF⊥x轴,通过△AOF∽△OBG可得结果;
②设直线x=-1与x轴交于H,且AF⊥X
于F,根据平行线的性质得到∠ABH=α由三角形函数得到tanα=![]() ,根据相似三角形的性质可得
,根据相似三角形的性质可得![]() ,于是得到二次函数,配方后根据二次函数的性质可求解.
,于是得到二次函数,配方后根据二次函数的性质可求解.
试题解析:⑴如图,在Rt△ABE中(4-y)2+42=52;
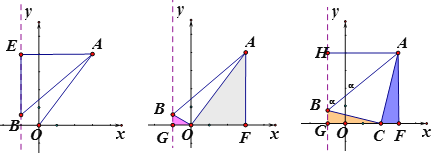
解得y=1或7 ∴B(-1,1)或B(-1,7)
⑵①易证△AOF∽△OBG
∴BO:AO=OG:AF=1:4 ∴tan∠BAC(或者tan∠BAO)=![]()
②由平行可知:∠ABH=α,在Rt△ABE中tanα=![]() ,
,
∵ tanα随BH的增大而减小,∴当BH最小时tanα有最大值;即BG最大时,tanα有最大值。
易证△ACF∽△CBG 得BG/CF=CG/AF y/x-3=x+1/4
y=-![]() (x+1)(3-x)=-
(x+1)(3-x)=-![]() (x-1)2+1
(x-1)2+1
当x=1时,ymax=1 当C(1,0)时,tanα有最大值![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(m+3,m-2)在直角坐标系的x轴上,则点P的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的顶点坐标为(1,2),且经过点(3,10)求这条抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面文字,然后按要求解题.
例:1+2+3+…+100=?如果一个一个顺次相加显然太麻烦,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.因为1+100=2+99=3+98=…=50+51=101,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果:
1+2+3+4+5+…+100
=(1+100)+(2+99)+(3+98)+…+(50+51)
=101× = .
(1)补全例题解题过程;
(2)请猜想:1+2+3+4+5+6+…+(2n﹣2)+(2n﹣1)+2n= .
(3)试计算:a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=(m-1)x-m+4的图象与y轴的交点在x轴的上方,则m的取值范围是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形的两条边长分别为2和6,那么这个三角形第三边的长可能是 ( )
A. 2B. 3C. 4D. 6.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=BC,D是AC中点,点O是AB上一点,⊙O过点B且与AC相切于点E,交BD于点G,交AB于点F.

(1)求证: BE平分∠ABD;
(2)当BD=2,sinC=
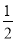 时,求⊙O的半径.
时,求⊙O的半径.
相关试题

