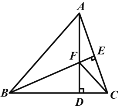
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=2,求AD的长.
参考答案:
【答案】(1)证明见解析;(2)AD=2+2![]() .
.
【解析】
(1)根据角边角定理证明△ADC≌△BDF,得AC=BF,根据等腰三角形三线合一的性质知AC=2AE,从而得BF=2AE;
(2)根据△ADC≌△BDF,得DF=CD,根据勾股定理得CF,根据线段垂直平分线上的点到线段两端点的距离相等得AF=CF,DF+AF即为AD的长.
(1)证明:∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形,∴AD=BD,
∵BE⊥AC,AD⊥BC,∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°
∴∠CAD=∠CBE,在△ADC和△BDF中,
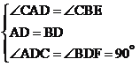 ,
,
∴△ADC≌△BDF(ASA),∴BF=AC,∵AB=BC,BE⊥AC,
∴AC=2AF,∴BF=2AE;
(2)解:∵△ADC≌△BDF,∴DF=CD=2,在Rt△CDF中,
![]() ,
,
∵BE⊥AC,AE=EC,∴AF=CF=2,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )

A.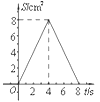
B.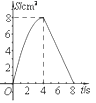
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:
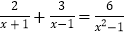
(2)计算:3a(2a2-9a+3)-4a(2a-1)
(3)计算:(
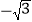 )×(
)×(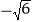 )+|
)+|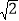 -1|+(5-2π)0
-1|+(5-2π)0(4)先化简,再求值:(xy2+x2y)
 ,其中x=
,其中x=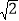 ,y=
,y= .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,方格图中每个小正方形的边长为1,点A、B、C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)直接写出AA1的长度;
(3)如图2,A、C是直线MN同侧固定的点,D是直线MN上的一个动点,在直线MN上画出点D,使AD+DC最小.(保留作图痕迹)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某地气象资料表明:当地雷雨持续的时间t(h)可以用下面的公式来估计:t2=
 ,其中d(km)是雷雨区域的直径.
,其中d(km)是雷雨区域的直径.(1)如果雷雨区域的直径为9km,那么这场雷雨大约能持续多长时间?
(2)如果一场雷雨持续了1h,那么这场雷雨区域的直径大约是多少(结果精确到0.1km)?
-
科目: 来源: 题型:
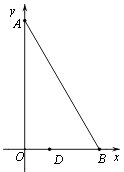
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A在y轴上,点B在x轴上,∠ABO=60°,若点D(1,0)且BD=2OD.把△ABO绕着点D逆时针旋转m°(0<m<180)后,点B恰好落在初始Rt△ABO的边上,此时的点B记为B′,则点B′的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3).
(1)求此二次函数的表达式,并用配方法将其化为y=a(x﹣h)2+k的形式;
(2)画出此函数图象的示意图.
相关试题

