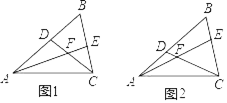
【题目】在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.
(1)如图1,若AE、CD为△ABC的角平分线:
①求∠AFD的度数;
②若AD=3,CE=2,求AC的长;
(2)如图2,若∠EAC=∠DCA=30°,求证:AD=CE.
参考答案:
【答案】(1)①60°;②5;(2)详见解析.
【解析】
(1)①根据角平分线的定义、三角形内角和定理计算;
②在AC上截取AG=AD=3,连接FG,证明△ADF≌△AGF、△CGF≌△CEF,根据全等三角形的性质解答;
(2)在AE上截取FH=FD,连接CH,证明△ADF≌△CHF,根据全等三角形的性质、三角形的外角的性质解答.
解:(1)①∵AE、CD分别为△ABC的角平分线,
∴∠FAC=![]() ∠BAC,∠FCA=
∠BAC,∠FCA=![]() ∠BCA,
∠BCA,
∵∠B=60°
∴∠BAC+∠BCA=120°,
∴∠AFC=180﹣∠FAC﹣∠FCA=180﹣![]() (∠BAC+∠BCA)=120°
(∠BAC+∠BCA)=120°
∴∠AFD=180°-∠AFC=60°;
②在AC上截取AG=AD=3,连接FG,
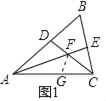
∵AE、CD分别为△ABC的角平分线,
∴∠FAC=∠FAD,∠FCA=∠FCE,
∵∠AFC=120°,
∴∠AFD=∠CFE=60°,
在△ADF和△AGF中,
∵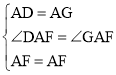 ,
,
∴△ADF≌△AGF(SAS),
∴∠AFD=∠AFG=60°,
∴∠GFC=∠CFE=60°,
在△CGF和△CEF中,
∵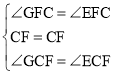 ,
,
∴△CGF≌△CEF(ASA),
∴CG=CE=2,
∴AC=5;
(2)在AE上截取FH=FD,连接CH,
∵∠FAC=∠FCA=30°,
∴FA=FC,
在△ADF和△CHF中,
∵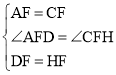 ,
,
∴△ADF≌△CHF(SAS),
∴AD=CH,∠DAF=∠HCF,
∵∠CEH=∠B+∠DAF=60°+∠DAF,
∠CHE=∠HAC+∠HCA=60°+∠HCF,
∴∠CEH=∠CHE,
∴CH=CE,
∴AD=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车沿同一平直公路由A地匀速行驶(中途不停留),前往终点B地,甲、乙两车之间的距离S(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.下列说法:
①甲、乙两地相距210千米;②甲速度为60千米/小时;③乙速度为120千米/小时;④乙车共行驶3 小时,其中正确的个数为( )
小时,其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强对校内外安全监控,创建平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.
甲型
乙型
价格(元/台)
a
b
有效半径(米/台)
150
100
(1)求a、b的值;
(2)若购买该批设备的资金不超过11000元,且要求监控半径覆盖范围不低于1600米,两种型号的设备均要至少买一台,请你为学校设计购买方案,并计算最低购买费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小青在本学期的数学成绩如下表所示(成绩均取整数):
测验类别
平时
期中考试
期末考试
测验1
测验1
测验1
课题学习
成绩
88
70
96
86
85


(1)计算小青本学期的平时平均成绩;
(2)如果学期的总评成绩是根据图所示的权重计算,那么本学期小青的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标?
-
科目: 来源: 题型:
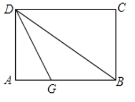
查看答案和解析>>【题目】如图,折叠长方形纸片ABCD,先折出折痕(对角线)BD,再折叠使AD边与BD重合,得折痕DG,若AB=4,BC=3,求AG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A(a,0),B(0,2
 )
)(1)点(k+1,2k﹣5)关于x轴的对称点在第一象限,a为实数k的范围内的最大整数,求A点的坐标及△AOB的面积;
(2)在(1)的条件下如图1,点P是第一象限内的点,且△ABP是以AB为腰的等腰直角三角形,请直接写出P点坐标;
(3)在(1)的条件下,如图2,以AB、OB的作等边△ABC和等边△OBD,连接AD、OC交于E点,连接BE.
①求证:EB平分∠CED;
②M点是y轴上一动点,求AM+CM最小时点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
相关试题

