【题目】在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,如果⊙O的半径为2 ![]() ,
,
①请你判断M(2,0),N(﹣2,﹣1)两个点的变换点与⊙O的位置关系;
②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+6上,求点P与⊙O上任意一点距离的最小值. 
参考答案:
【答案】
(1)解:①M(2,0)的变换点M′的坐标为(2,2),则OM′= ![]() =2
=2 ![]() ,所以点M(2,0)的变换点在⊙O上;
,所以点M(2,0)的变换点在⊙O上;
N(﹣2,﹣1)的变换点N′的坐标为(﹣3,﹣1),则ON′= ![]() =
= ![]() >2
>2 ![]() ,所以点N(﹣2,﹣1)的变换点在⊙O外;
,所以点N(﹣2,﹣1)的变换点在⊙O外;
②设P点坐标为(x,x+2),则P点的变换点为P′的坐标为(2x+2,﹣2),则OP′= ![]() ,
,
∵点P′在⊙O的内,
∴ ![]() <2
<2 ![]() ,
,
∴(2x+2)2<4,即(x+1)2<1,
∴﹣1<x+1<1,解得﹣2<x<0,
即点P横坐标的取值范围为﹣2<x<0
(2)解:设点P′的坐标为(x,﹣2x+6),P(m,n),
根据题意得m+n=x,m﹣n=﹣2x+6,
∴3m+n=6,
即n=﹣3m+6,
∴P点坐标为(m,﹣3m+6),
∴点P在直线y=﹣3x+6上,
设直线y=﹣3x+6与x轴相交于点A,与y轴相交于点B,过O点作OH⊥AB于H,交⊙O于C,如图2,
则A(2,0),B(0,6),
∴AB= ![]() =2
=2 ![]() ,
,
∵ ![]() OHAB=
OHAB= ![]() OAOB,
OAOB,
∴OH= ![]() =
= ![]() ,
,
∴CH= ![]() ﹣1,
﹣1,
即点P与⊙O上任意一点距离的最小值为 ![]() ﹣1.
﹣1.
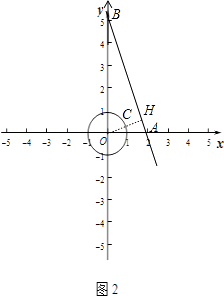
【解析】(1)①根据新定义得到点M的变换点M′的坐标为(2,2),于是根据勾股定理计算出OM′=2 ![]() ,则根据点与圆的位置关系的判定方法可判断点M的变换点在⊙O上;同样方法可判断点N(﹣2,﹣1)的变换点在⊙O外
,则根据点与圆的位置关系的判定方法可判断点M的变换点在⊙O上;同样方法可判断点N(﹣2,﹣1)的变换点在⊙O外
②利用一次函数图象上点的坐标特征,设P点坐标为(x,x+2),利用新定义得到P点的变换点为P′的坐标为(2x+2,﹣2),则根据勾股定理计算出OP′= ![]() ,然后利用点与圆的位置关系得到
,然后利用点与圆的位置关系得到 ![]() <2
<2 ![]() ,解不等式得﹣2<x<0;(2)设点P′的坐标为(x,﹣2x+6),P(m,n),根据新定义得到m+n=x,m﹣n=﹣2x+6,消去x得3m+n=6,则n=﹣3m+6,于是得到P点坐标为(m,﹣3m+6),则可判断点P在直线y=﹣3x+6上,设直线y=﹣3x+6与x轴相交于点A,与y轴相交于点B,过O点作OH⊥AB于H,交⊙O于C,如图2,易得A(2,0),B(0,6),利用勾股定理计算出AB=2
,解不等式得﹣2<x<0;(2)设点P′的坐标为(x,﹣2x+6),P(m,n),根据新定义得到m+n=x,m﹣n=﹣2x+6,消去x得3m+n=6,则n=﹣3m+6,于是得到P点坐标为(m,﹣3m+6),则可判断点P在直线y=﹣3x+6上,设直线y=﹣3x+6与x轴相交于点A,与y轴相交于点B,过O点作OH⊥AB于H,交⊙O于C,如图2,易得A(2,0),B(0,6),利用勾股定理计算出AB=2 ![]() ,再利用面积法计算出OH=
,再利用面积法计算出OH= ![]() ,所以CH=
,所以CH= ![]() ﹣1,当点P在H点时,PC为点P与⊙O上任意一点距离的最小值.
﹣1,当点P在H点时,PC为点P与⊙O上任意一点距离的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数
 的图象与x轴,y轴分别交于点A、B,与函数
的图象与x轴,y轴分别交于点A、B,与函数 的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数
的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数 和
和 的图象于点C、D.
的图象于点C、D.(1)求点M、点A的坐标;
(2)若OB=CD,求a的值,并求此时四边形OPCM的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC和△CDE都是等腰直角三角形,∠C=90°,将△CDE绕点C逆时针旋转一个角度α(0°<α<90°),使点A,D,E在同一直线上,连接AD,BE.
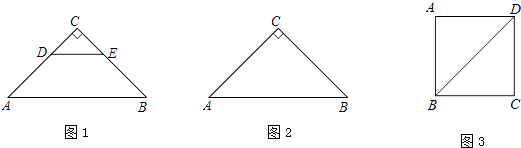
(1)①依题意补全图2;
②求证:AD=BE,且AD⊥BE;
③作CM⊥DE,垂足为M,请用等式表示出线段CM,AE,BE之间的数量关系;
(2)如图3,正方形ABCD边长为 ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】纸箱厂用如图1所示的长方形和正方形纸板,做成如图2所示的竖式与横式两种长方体形状的有底无盖纸盒.

(1)现有正方形纸板172张,长方形纸板330张.若要做两种纸盒共l00个,设做竖式纸盒x个.
①根据题意,完成以下表格:
 纸盒
纸盒
纸板竖式纸盒(个)
横式纸盒(个)
x
正方形纸板(张)
2(100-x)
长方形纸板(张)
4x
②按两种纸盒的数量分,有哪几种生产方案?
(2)若有正方形纸板112张,长方形纸板
 张,做成上述两种纸盒,纸板恰好用完.已知100<
张,做成上述两种纸盒,纸板恰好用完.已知100< <110,则
<110,则 的值是 .
的值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣x2+(m﹣1)x+m与y轴交点坐标是(0,3).
(1)求出m的值并画出这条抛物线;
(2)求抛物线与x轴的交点和抛物线顶点的坐标;
(3)当x取什么值时,y的值随x值的增大而减小? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠A=22.5°,CD=8cm,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.

(1)画出将△ABC向右平移2个单位后得到的△A1B1C1 , 再画出将△A1B1C1绕点B1按逆时针方向旋转90°后所得到的△A2B1C2;
(2)求线段B1C1旋转到B1C2的过程中,点C1所经过的路径长.
相关试题

