【题目】在菱形ABCD中,AC是对角线.
(1)如图①,若AB=6,则菱形ABCD的周长为______;若∠DAB=70,则∠D的度数是_____;∠DCA的度数是____;
(2)如图②,P是AB上一点,连接DP交对角线AC于点E,连接EB,求证: ∠APD=∠EBC.

参考答案:
【答案】(1)24;110°;35°;(2)见解析.
【解析】
(1)由菱形的性质可求解;
(2)由“SAS”可得△DCE≌△BCE,可得∠CDP=∠CBE,由平行线的性质可得∠CDP=∠APD=∠CBE.
解:(1)∵四边形ABCD是菱形
∴AB=BC=CD=AD=6,∠DAB+∠ADC=180°,
∠DCA=![]() ∠DCB=
∠DCB=![]() ∠DAB=35°
∠DAB=35°
∴菱形ABCD的周长=4×6=24,
∠ADC=180°-70°=110°,
故答案为:24,110°,35°
(2)证明:∵菱形ABCD
∴CD//AB,CD=CB,CA平分∠BCD
∴∠CDE=∠APD,∠ACD=∠ACB
∵CD=CB,∠BCE=∠DCE,CE=CE
∴△CBE≌△CDE(SAS)
∴∠CBE=∠CDE
∴∠CBE=∠APD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,⊙O与AC相交于点D,∠BAC=45°,AB=BC.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为2cm,求图中阴影部分的面积.

-
科目: 来源: 题型:
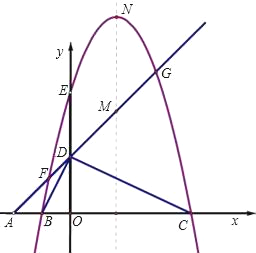
查看答案和解析>>【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF相交于点O,下列结论:
①∠DOC=90°,②OC=OE,③tan∠OCD=
 ,④△COD的面积等于四边形BEOF的面积,正确的有 ( )
,④△COD的面积等于四边形BEOF的面积,正确的有 ( )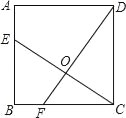
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC与△ABD不全等,且AC=AD=1,∠ABD=∠ABC=45°,∠ACB=60°,则CD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若多项式2x3﹣8x2y+x+1与多项式﹣3x3﹣2mx2y+6x﹣9的差的值与字母y的取值无关,求m的值.
(2)已知有理数a,b,c在数轴上对应位置如图所示,化简:|a+b|﹣|b+c|+|a+c|.
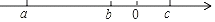
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,小明在封闭图形内划出了一个半径为1米的圆,在不远处向圈内掷石子,且记录如下:

依此估计此封闭图形ABC的面积是_____m2.
相关试题

