【题目】已知△ABC与△ABD不全等,且AC=AD=1,∠ABD=∠ABC=45°,∠ACB=60°,则CD= .
参考答案:
【答案】1或![]() .
.
【解析】分析:
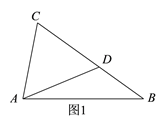
由题意可知本题存在两种可能情况:(1)如图1,C、D两点在线段AB的同侧,此时由已知条件易证△ACD是等边三角形,由此即可求得CD的长;(2)如图2,C、D两点在线段AB的两侧,此时由已知条件可知将△ABD沿AB翻折,点D的对应点D′刚好落在BC边上,连接CD,由已知条件可证得∠CAD=90°,从而可在Rt△ACD中由勾股定理求得CD的长.
详解:
(1)如图1,当C、D在AB同侧时,
∵AC=AD=1,∠C=60°,
∴△ACD是等边三角形,
∴CD=AC=1;
(2)如图2,当C、D在AB两侧时,
∵∠ABC=∠ABD=45°,
∴把△ABD沿AB翻折得到△ABD′时,点D′在BC边上,
由(1)可知,此时△ACD′是等边三角形,
∴∠AD′C=60°,
∴∠AD′B=120°,
∴∠ADB=120°,
又∵在四边形ADBC中,∠ACB=60°,∠DBC=∠ABC+∠ABD=90°,
∴∠CAD=360°-60°-120°-90°=90°,
∴在Rt△ACD中,CD=![]() .
.

综上所述可得CD的长为1或![]() .
.
故答案为:1或![]() .
.
-
科目: 来源: 题型:
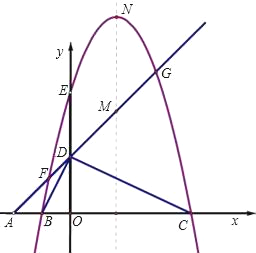
查看答案和解析>>【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF相交于点O,下列结论:
①∠DOC=90°,②OC=OE,③tan∠OCD=
 ,④△COD的面积等于四边形BEOF的面积,正确的有 ( )
,④△COD的面积等于四边形BEOF的面积,正确的有 ( )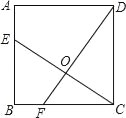
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,AC是对角线.
(1)如图①,若AB=6,则菱形ABCD的周长为______;若∠DAB=70,则∠D的度数是_____;∠DCA的度数是____;
(2)如图②,P是AB上一点,连接DP交对角线AC于点E,连接EB,求证: ∠APD=∠EBC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若多项式2x3﹣8x2y+x+1与多项式﹣3x3﹣2mx2y+6x﹣9的差的值与字母y的取值无关,求m的值.
(2)已知有理数a,b,c在数轴上对应位置如图所示,化简:|a+b|﹣|b+c|+|a+c|.
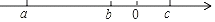
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,小明在封闭图形内划出了一个半径为1米的圆,在不远处向圈内掷石子,且记录如下:

依此估计此封闭图形ABC的面积是_____m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴按下图中的方式搭图形:

(1)按图示规律补全表格:
图形编号
①
②
③
④
⑤
火柴棒根数
7
12
(2)按照这种方式搭下去,请写出搭第n个图形需要的火柴根数;
(3)小明发现:按照这种方式搭图形会产生若干个正方形,若使用187根火柴搭图形,图中会产生多少个正方形?
相关试题

