搜索
【题目】如图，有一矩形纸片ABCD，AB=8，AD=17，将此矩形纸片折叠，使顶点A落在BC边的A′处，折痕所在直线同时经过边AB、AD（包括端点），设BA′=x，则x的取值范围是 .
参考答案：
【答案】
【解析】
试题作出图形，根据矩形的对边相等可得BC=AD，CD=AB，当折痕经过点D时，根据翻折的性质可得A′D=AD，利用勾股定理列式求出A′C，再求出BA′；当折痕经过点B时，根据翻折的性质可得BA′=AB，此两种情况为BA′的最小值与最大值的情况，然后写出x的取值范围即可．
试题解析：
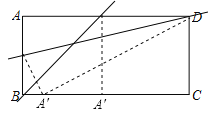
如图，∵四边形ABCD是矩形，AB=8，AD=17，
∴BC=AD=17，CD=AB=8，
①当折痕经过点D时，
由翻折的性质得，A′D=AD=17，在Rt△A′CD中，A′C=15 ∴BA′=BC-A′C=17-15=2；
②当折痕经过点B时，由翻折的性质得，BA′=AB=8，
∴x的取值范围是2≤x≤8．
故答案为：2≤x≤8．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将周长为8的△ABC沿BC方向平移1个单位长度得到
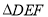，则四边形
的周长为（ ）
A. 8 B. 10 C. 12 D. 16
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个平行四边形的一条边长为5，两条对角线的长分别为6和8，则它的面积为________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场将每件进价为80元的某种商品原来按每件100元出售，一天可售出100件．后来经过市场调查，发现这种商品单价每降低1元，其销量可增加10件．
（1）求商场经营该商品原来一天可获利润多少元？
（2）设后来该商品每件降价x元，，商场一天可获利润y元．
①若商场经营该商品一天要获利润2160元，则每件商品应降价多少元？
②求出y与x之间的函数关系式，结合题意写出当x取何值时，商场获利润不少于2160元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，∠B=∠AFE，EA是∠BEF的平分线，求证：
(1)△ABE≌△AFE；
(2)∠FAD=∠CDE.
-
科目： 来源： 题型：
查看答案和解析>>【题目】建立模型：
如图1，已知△ABC，AC=BC，∠C=90°，顶点C在直线l上．
操作：
过点A作AD⊥l于点D，过点B作BE⊥l于点E．求证：△CAD≌△BCE．
模型应用：
（1）如图2，在直角坐标系中，直线l1：y=
x+4与y轴交于点A，与x轴交于点B，将直线l1绕着点A顺时针旋转45°得到l2．求l2的函数表达式．（2）如图3，在直角坐标系中，点B（8，6），作BA⊥y轴于点A，作BC⊥x轴于点C，P是线段BC上的一个动点，点Q（a，2a﹣6）位于第一象限内．问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形，若能，请求出此时a的值，若不能，请说明理由．
-
科目： 来源： 题型：
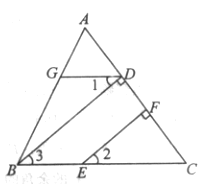
查看答案和解析>>【题目】如图，已知BD⊥AC，EF⊥AC，垂足分别为D、F，∠1＝∠2，请将证明∠ADG＝∠C过程填写完整．
证明：BD⊥AC，EF⊥AC（已知）
∴∠BDC＝∠EFC＝90°
∴BD∥
∠2＝∠3
又∵∠1＝∠2（已知）
∴∠1＝∠3（等量代换）
∴DG∥
∴∠ADG＝∠C
相关试题
