【题目】如图①,梯形ABCD中,AD∥BC,∠C=90°,BA=BC.动点E、F同时从点B出发,点E沿折线 BA–AD–DC运动到点C时停止运动,点F沿BC运动到点C时停止运动,它们运动时的速度都是1 cm/s.设E出发t s时,△EBF的面积为y cm2.已知y与t的函数图象如图②所示,其中曲线OM为抛物线的一部分,MN、NP为线段.
请根据图中的信息,解答下列问题:
(1)AD= cm,BC= cm;
(2)求a的值,并用文字说明点N所表示的实际意义;
(3)直接写出当自变量t为何值时,函数y的值等于5.

参考答案:
【答案】(1)AD=2cm,BC=5cm;(2)a=10,点N所表示的实际意义:当点E运动7s时到达点D,此时点F沿BC已运动到点C并停止运动,这时△EBF的面积为10 cm2;(3)![]() 或9.
或9.
【解析】试题分析:(1)此题的关键是要理解分段函数的意义,OM段是曲线,说明E、F分别在BA、BC上运动,此时y、t的关系式是二次函数;MN段是线段,且平行于t轴,那么此时F运动到终点C,且E在线段AD上运动,此时y为定值;NP段是线段,此时y、t的函数关系式是一次函数,此时E在线段CD上运动,此时y值随t的增大而减小;根据上面的分析,可知在MN之间时,E在线段AD上运动,在这个区间E点运动了2秒,所以AD=2cm;根据OM段的函数图象知:当t=5时,E、F分别运动到A、C两点,那么AB=BC=5;
试题解析:(1)由图可知:OM段为抛物线,此时点E、F分别在BA、BC上运动;
当E、A重合,F、C重合时,t=5s,
∴AB=BC=5cm;
(2)过A作AH⊥BC,H为垂足,由已知BH=3,BA=BC=5,
∴AH="4"
∴当点E、F分别运动到A、C时△EBF的面积为: ![]() ×BC×AH=
×BC×AH=![]() ×5×4=10,
×5×4=10,
即a的值为10,
点N所表示的实际意义:当点E运动7s时到达点D,此时点F沿BC已运动到点C 并停止运动,这时△EBF的面积为10 cm2;
(3)当点E在BA上运动时,设抛物线的解析式为y=at2,把M点的坐标(5,10)代入得a=![]() ,
,
∴y=![]() t2,0<t≤5;
t2,0<t≤5;
当点E在DC上运动时,设直线的解析式为y=kt+b,
把P(11,0),N(7,10)代入,得11k+b=0,7k+b=10,解得k=-![]() ,b=
,b=![]() ,
,
所以y=-![]() t+
t+![]() ,(7≤t<11)
,(7≤t<11)
把y=5分别代入y=![]() t2和y=-
t2和y=-![]() t+
t+![]() 得,5=
得,5=![]() t2和5=-
t2和5=-![]() t+
t+![]() ,解得:t=
,解得:t=![]() 或t=9.
或t=9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.
(1)求证:直线DE是⊙O的切线;
(2)若 BF=10,sin∠BDE=
 ,求DE的长.
,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面内给定射线OA,射线OB及∠MON,给出如下定义:若由射线OA、OB组成的∠AOB的平分线OT落在∠MON的内部或边OM、ON上,则称射线OA与射线OB关于∠MON内含对称.例如,图1中射线OA与射线OB关于∠MON内含对称

已知:如图2,在平面内,∠AOM=10°,∠MON=20°
(1)若有两条射线
 ,
, 的位置如图3所示,且
的位置如图3所示,且 ,
, ,则在这两条射线中,与射线OA关于∠MON内含对称的射线是_____________
,则在这两条射线中,与射线OA关于∠MON内含对称的射线是_____________(2)射线OC是平面上绕点O旋转的一条动射线,若射线OA与射线OC关于∠MON内含对称,设∠COM=x°,求x的取值范围;
(3)如图4,∠AOE=∠EOH=2∠FOH=20°,现将射线OH绕点O以每秒1°的速度顺时针旋转,同时将射线OE和OF绕点O都以每秒3°的速度顺时针旋转.设旋转的时间为t秒,且
 .若∠FOE的内部及两边至少存在一条以O为顶点的射线与射线OH关于∠MON内含对称,直接写出t的取值范围.
.若∠FOE的内部及两边至少存在一条以O为顶点的射线与射线OH关于∠MON内含对称,直接写出t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
让我们来规定一种运算:
 ,
, 例如:
 ,再如:
,再如:
按照这种运算的规定:请解答下列各个问题:
①
 ;
; ② 当
 = 时,
= 时, 
 =0;
=0;③ 将下面式子进行因式分解:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ΔABC内接于⊙O,AB为⊙O的直径,BD⊥AB,交AC的延长线于点D.
(1)若E是BD的中点,连结CE,试判断CE与⊙O的位置关系.
(2)若AC=3CD,求∠A的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D为AB边上的一点,∠A=36°,AC=BC,AC2=ADAB.

(1)求证:△ADC和△BDC都是等腰三角形;
(2)若AB=1,求AC的值(精确到0.001).
-
科目: 来源: 题型:
查看答案和解析>>【题目】边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.
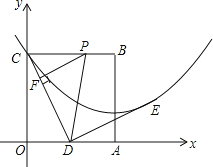
(1)求抛物线的解析式;
(2)点P从点C出发,沿射线CB每秒1个单位长度的速度运动,运动时间为t秒.过点P作PF⊥CD于点F,当t为何值时,以点P,F,D为顶点的三角形与△COD相似?
(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.
相关试题

