Question

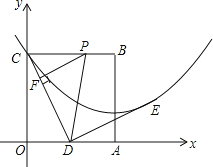
【题目】边长为2的正方形OABC在平面直角坐标系中的位置如图所示，点D是边OA的中点，连接CD，点E在第一象限，且DE⊥DC，DE=DC．以直线AB为对称轴的抛物线过C，E两点．

（1）求抛物线的解析式；

（2）点P从点C出发，沿射线CB每秒1个单位长度的速度运动，运动时间为t秒．过点P作PF⊥CD于点F，当t为何值时，以点P，F，D为顶点的三角形与△COD相似？

（3）点M为直线AB上一动点，点N为抛物线上一动点，是否存在点M，N，使得以点M，N，D，E为顶点的四边形是平行四边形？若存在，请直接写出满足条件的点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）1或；（3）M1（2，1），N1（4，2）或M2（2，3），N2（0，2）或M3（2，），N3（2，）．

【解析】

试题分析：（1）根据正方形的性质，可得OA=OC，∠AOC=∠DGE，根据余角的性质，可得∠OCD=∠GDE，根据全等三角形的判定与性质，可得EG=OD=1，DG=OC=2，根据待定系数法，可得函数解析式；

（2）分类讨论：若△DFP∽△COD，根据相似三角形的性质，可得∠PDF=∠DCO，根据平行线的判定与性质，可得∠PDO=∠OCP=∠AOC=90，根据矩形的判定与性质，可得PC的长；若△PFD∽△COD，根据相似三角形的性质，可得∠DPF=∠DCO，=，根据等腰三角形的判定与性质，可得DF于CD的关系，根据相似三角形的相似比，可得PC的长；

（3）分类讨论：MDNE，MNDE，NDME，根据一组对边平行且相等的四边形式平行四边，可得答案．

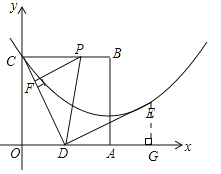
试题解析：（1）过点E作EG⊥x轴于G点．∵四边形OABC是边长为2的正方形，D是OA的中点，∴OA=OC=2，OD=1，∠AOC=∠DGE=90°，∵∠CDE=90°，∴∠ODC+∠GDE=90°，∵∠ODC+∠OCD=90°，∴∠OCD=∠GDE，在△OCD和△GED中，∵∠COD=∠DGE，∠OCD=∠GDE，DC=DE，∴△ODC≌△GED（AAS），∴EG=OD=1，DG=OC=2，∴点E的坐标为（3，1），∵抛物线的对称轴为直线AB即直线x=2，∴可设抛物线的解析式为，将C、E点的坐标代入解析式，得：，解得：，抛物线的解析式为；

（2）①若△DFP∽△COD，则∠PDF=∠DCO，∴PD∥OC，∴∠PDO=∠OCP=∠AOC=90°，∴四边形PDOC是矩形，∴PC=OD=1，∴t=1；

②若△PFD∽△COD，则∠DPF=∠DCO，=，∴∠PCF=90°﹣∠DCO=90﹣∠DPF=∠PDF，∴PC=PD，∴DF=CD，∵，∴CD=，∴DF=，∵=，∴PC=PD=×=，t=，

综上所述：t=1或t=时，以点P，F，D为顶点的三角形与△COD相似；

（3）存在，

四边形MDEN是平行四边形时，M1（2，1），N1（4，2）；

四边形MNDE是平行四边形时，M2（2，3），N2（0，2）；

四边形NDME是平行四边形时，M3（2，），N3（2，）．