【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,AD是∠BAC的平分线.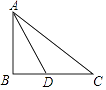
(1)尺规作图:过点D作DE⊥AC于E;
(2)求DE的长.
参考答案:
【答案】
(1)
解:方法1,如图1所示,过点D作AC的垂线即可;
方法2:运用角平分线的性质,以点D为圆心,BD的长为半径画圆,⊙D和AC相切于点E,连接DE即可.

(2)
解:方法一:设DE=x,则AC= ![]() =5.
=5.
∵AD是∠BAC的平分线,∠ABC=90°,DE⊥AC,
∴BD=DE=x,CD=BC﹣BD=4﹣x.
∵S△ACD= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,解得x=
,解得x= ![]() ,
,
∴DE=x= ![]() .
.
方法二:设DE=x,则AC= ![]() =5.
=5.
∵AD是∠BAC的平分线,∠ABC=90°,DE⊥AC,
∴BD=DE=x,CD=BC﹣BD=4﹣x.
∵∠DEC=∠ABC=90°,∠C=∠C,
∴△DEC∽△ABC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,解得x=
,解得x= ![]() ,
,
∴DE=x= ![]() .
.
方法三:设DE=x,则AC= ![]() =5.
=5.
∵AD是∠BAC的平分线,∠ABC=90°,DE⊥AC,
∴BD=DE=x,CD=BC﹣BD=4﹣x.
∵在Rt△ABC中,sin∠C= ![]() =
= ![]() ,
,
在Rt△DEC中,sin∠C= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,解得x=
,解得x= ![]() ,
,
∴DE=x= ![]() .
.
【解析】(1)根据过直线外一点作直线垂线的作法即可画出图形;(2)设DE=x,则AC= ![]() =5,跟进吧AD是∠BAC的平分线,∠ABC=90°,DE⊥AC可得出BD=DE=x,CD=BC﹣BD=4﹣x,再由S△ACD=
=5,跟进吧AD是∠BAC的平分线,∠ABC=90°,DE⊥AC可得出BD=DE=x,CD=BC﹣BD=4﹣x,再由S△ACD= ![]() =
= ![]() 求出x的值即可.
求出x的值即可.
【考点精析】利用角平分线的性质定理对题目进行判断即可得到答案,需要熟知定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为( )
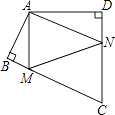
A.80°
B.90°
C.100°
D.130° -
科目: 来源: 题型:
查看答案和解析>>【题目】求下列各式中的x:
(1)16x2-361=0; (2)(x-1)2=25;
(3)27
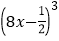 =216; (4)
=216; (4)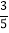 (x-2)3=
(x-2)3=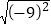 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年3月全国两会胜利召开,某学校就两会期间出现频率最高的热词:A.蓝天保卫战,B.不动产保护,C.经济增速,D.简政放权等进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
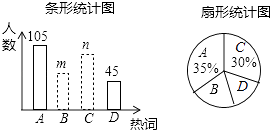
(1)本次调查中,一共调查了名同学;
(2)条形统计图中,m= , n=;
(3)从该校学生中随机抽取一个最关注热词D的学生的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某地开辟一块长方形的荒地用于新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍,它的面积为400 000 m2,那么:
(1)荒地的宽是多少?有1 000 m吗?(结果保留一位小数)
(2)如果要求结果保留整数,那么宽大约是多少?
(3)计划在该公园中心建一个圆形花圃,面积是800 m2,你能估计它的半径吗?(要求结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根A型跳绳和1根B型跳绳共需56元,1根A型跳绳和2根B型跳绳共需82元.
(1)求一根A型跳绳和一根B型跳绳的售价各是多少元?
(2)学校准备购进这两种型号的跳绳共50根,并且A型跳绳的数量不多于B型跳绳数量的3倍,请设计书最省钱的购买方案,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于下列各组条件,不能判定△
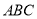 ≌△
≌△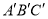 的一组是 ( )
的一组是 ( )A. ∠A=∠A′,∠B=∠B′,AB=A′B′
B. ∠A=∠A′,AB=A′B′,AC=A′C′
C. ∠A=∠A′,AB=A′B′,BC=B′C′
D. AB=A′B′,AC=A′C′,BC=B′C′
相关试题

