【题目】在Rt△ABC中,∠C=90°,AC=4,BC=3,若以C为圆心,R为半径作的圆与直线AB相切,则R=______.
参考答案:
【答案】2.4
【解析】
首先根据勾股定理求斜边长,再利用三角形面积求斜边上的高,再根据直线与圆的位置关系求半径R.
解:过C作CD⊥AB于D.
∵AB2=AC2+BC2,AC=3,BC=4,
∴AB2=32+42=25,
∴AB=5,
根据三角形面积,得
AC·BC=CD·AB
∴CD=2.4.
∵直线AB和⊙C相切,
∴R=CD=2.4.
-
科目: 来源: 题型:
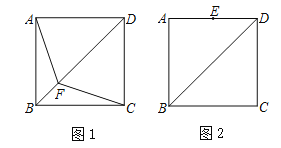
查看答案和解析>>【题目】已知:如图,正方形ABCD中,点F是对角线BD上的一个动点.
(1)如图1,连接AF,CF,直接写出AF与CF的数量关系;
(2)如图2,点E为AD边的中点,当点F运动到线段EC上时,连接AF,BE相交于点O.
①请你根据题意在图2中补全图形;
②猜想AF与BE的位置关系,并写出证明此猜想的思路;
③如果正方形的边长为2,直接写出AO的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
 =
= x-3与方程3n
x-3与方程3n =3(x+n)-2n的解相同,求(2n-27)2的值.
=3(x+n)-2n的解相同,求(2n-27)2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(3a﹣2)﹣3(a﹣5)
(2)(4a2b﹣5ab2)﹣(3a2b﹣4ab2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a+2|与(b﹣3)2 互为相反数,求 ab+3(a﹣b)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)-2x-
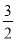 =x+
=x+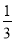 ;
;(2)3(5x-6)=3-20x;
(3)
 +
+ =x-1;
=x-1;(4)
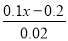 -
-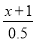 =3.
=3. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E.
(1)求证:△ABD≌△EBD;
(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.

相关试题

