Question

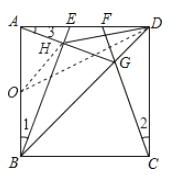
【题目】如图，E，F是正方形ABCD的边AD上两个动点，满足AE＝DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为1，则线段DH长度的最小值是_______．

Answer 1

【答案】

【解析】

根据正方形的性质可得AB=AD=CD，∠BAD=∠CDA，∠ADG=∠CDG，然后利用“边角边”证明△ABE和△DCF全等，根据全等三角形对应角相等可得∠1=∠2，利用“SAS”证明△ADG和△CDG全等，根据全等三角形对应角相等可得∠2=∠3，从而得到∠1=∠3，然后求出∠AHB=90°，取AB的中点O，连接OH、OD，根据直角三角形斜边上的中线等于斜边的一半可得OH=AB=，利用勾股定理列式求出OD，然后根据三角形的三边关系可知当O、D、H三点共线时，DH的长度最小．

解：在正方形ABCD中，AB=AD=CD，∠BAD=∠CDA，∠ADG=∠CDG，
在△ABE和△DCF中，

，

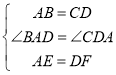∴△ABE≌△DCF（SAS），
∴∠1=∠2，
在△ADG和△CDG中，

，

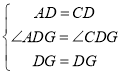∴△ADG≌△CDG（SAS），
∴∠2=∠3，
∴∠1=∠3，
∵∠BAH+∠3=∠BAD=90°，
∴∠1+∠BAH=90°，
∴∠AHB=180°-90°=90°，
取AB的中点O，连接OH、OD，

则OH=AO=AB=，

在Rt△AOD中，OD=，
根据三角形的三边关系，OH+DH＞OD，
∴当O、D、H三点共线时，DH的长度最小，
最小值=ODOH=．