【题目】如图,AB是⊙O的直径,BC切⊙O于点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F.

(1)试判断∠CBD与∠CEB是否相等,并证明你的结论;
(2)求证:![]() ;
;
(3)若BC=![]() AB,求tan∠CDF的值.
AB,求tan∠CDF的值.
参考答案:
【答案】(1)∠CBD与∠CEB相等,证明见解析;(2)证明见解析;(3)tan∠CDF=![]() .
.
【解析】试题分析:
(1)由AB是⊙O的直径,BC切⊙O于点B,可得∠ADB=∠ABC=90°,由此可得∠A+∠ABD=∠ABD+∠CBD=90°,从而可得∠A=∠CBD,结合∠A=∠CEB即可得到∠CBD=∠CEB;
(2)由∠C=∠C,∠CEB=∠CBD,可得∠EBC=∠BDC,从而可得△EBC∽△BDC,再由相似三角形的性质即可得到结论;
(3)设AB=2x,结合BC=![]() AB,AB是直径,可得BC=3x,OB=OD=x,再结合∠ABC=90°,
AB,AB是直径,可得BC=3x,OB=OD=x,再结合∠ABC=90°,
可得OC=![]() x,CD=(
x,CD=(![]() -1)x;由AO=DO,可得∠CDF=∠A=∠DBF,从而可得△DCF∽△BCD,由此可得:
-1)x;由AO=DO,可得∠CDF=∠A=∠DBF,从而可得△DCF∽△BCD,由此可得:![]() =
=![]() =
=![]() ,这样即可得到tan∠CDF=tan∠DBF=
,这样即可得到tan∠CDF=tan∠DBF=![]() =
=![]() .
.
试题解析:
(1)∠CBD与∠CEB相等,理由如下:
∵BC切⊙O于点B,
∴∠CBD=∠BAD,
∵∠BAD=∠CEB,
∴∠CEB=∠CBD,
(2)∵∠C=∠C,∠CEB=∠CBD,
∴∠EBC=∠BDC,
∴△EBC∽△BDC,
∴![]() ;
;
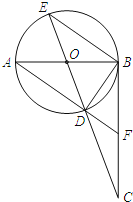
(3)设AB=2x,∵BC=![]() AB,AB是直径,
AB,AB是直径,
∴BC=3x,OB=OD=x,
∵∠ABC=90°,
∴OC=![]() x,
x,
∴CD=(![]() -1)x,
-1)x,
∵AO=DO,
∴∠CDF=∠A=∠DBF,
∴△DCF∽△BCD,
∴![]() =
=![]() =
=![]() ,
,
∵tan∠DBF=![]() =
=![]() ,
,
∴tan∠CDF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的弦CD与直径AB垂直于F,点E在CD上,且AE=CE.

(1)求证:CA2=CE CD;
(2)已知CA=5,EC=3,求sin∠EAF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形,如图,在△CFE中,CF=6,CE=12,∠FCE=45°,以点C为圆心,以任意长为半径作AD,再分别以点A和点D为圆心,大于
 AD长为半径做弧,交EF于点B,AB∥CD.
AD长为半径做弧,交EF于点B,AB∥CD.
(1)求证:四边形ACDB为△CFE的亲密菱形;
(2)求四边形ACDB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 分别与x轴、y轴交于
分别与x轴、y轴交于 两点,与直线
两点,与直线 交于点C(4,2).
交于点C(4,2).(1)点A坐标为( , ),B为( , );
(2)在线段
 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形 是平行四边形;
是平行四边形;(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得
 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为___.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△BOD都是等腰直角三角形,∠ACB=∠BDO=90°,且点A在反比例函数
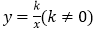 的图象上,若
的图象上,若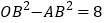 ,则k的值为 ____.
,则k的值为 ____. 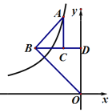
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
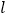 ∥AB,
∥AB,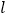 与 AB 之间的距离为 2 ,C、D 是直线
与 AB 之间的距离为 2 ,C、D 是直线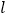 上
上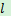 两个动点(点 C在 D 点的左侧),且 AB=CD=5.连接 AC、BC、BD,将△ABC 沿 BC 折叠得到△A′BC.若以 A′、C、B、D 为顶点的四边形为矩形,则此矩形相邻两边之和为____.
两个动点(点 C在 D 点的左侧),且 AB=CD=5.连接 AC、BC、BD,将△ABC 沿 BC 折叠得到△A′BC.若以 A′、C、B、D 为顶点的四边形为矩形,则此矩形相邻两边之和为____.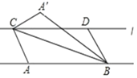
相关试题

