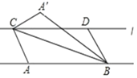
【题目】如图,已知直线![]() ∥AB,
∥AB,![]() 与 AB 之间的距离为 2 ,C、D 是直线
与 AB 之间的距离为 2 ,C、D 是直线![]() 上
上![]() 两个动点(点 C在 D 点的左侧),且 AB=CD=5.连接 AC、BC、BD,将△ABC 沿 BC 折叠得到△A′BC.若以 A′、C、B、D 为顶点的四边形为矩形,则此矩形相邻两边之和为____.
两个动点(点 C在 D 点的左侧),且 AB=CD=5.连接 AC、BC、BD,将△ABC 沿 BC 折叠得到△A′BC.若以 A′、C、B、D 为顶点的四边形为矩形,则此矩形相邻两边之和为____.
参考答案:
【答案】3![]() 或 7
或 7
【解析】
根据平行四边形的判定方法可得到四边形ABCD为平行四边形,当∠CBD=90°,则∠BCA=90°,由于S△A1CB=S△ABC=5,则S矩形A′CBD=10,根据勾股定理和完全平方公式进行计算;当∠BCD=90°,则∠CBA=90°,易得BC=2,而CD=5可得计算出结果.
∵AB=CD=5,AB∥CD,
∴四边形ABCD为平行四边形,
∴四边形ABDC的面积=2×5=10,
设矩形的边长分别为a,b,
当∠CBD=90°,
∵四边形ABDC是平行四边形,
∴∠BCA=90°,
∴S△A′CB=S△ABC=![]() ×2×5=5,
×2×5=5,
∴S矩形A′CBD=10,即ab=10,
而BA′=BA=5,
∴a2+b2=25,
∴(a+b)2=a2+b2+2ab=45,
∴a+b=3![]() ,
,
当∠BCD=90°时,
∵四边形ABDC是平行四边形,
∴∠CBA=90°,
∴BC=2,
而CD=5,
∴(a+b)2=(2+5)2=49,
∴a+b=7,
∴此矩形相邻两边之和为3![]() 或7.
或7.
故答案是:3![]() 或7.
或7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC切⊙O于点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F.

(1)试判断∠CBD与∠CEB是否相等,并证明你的结论;
(2)求证:
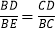 ;
;(3)若BC=
 AB,求tan∠CDF的值.
AB,求tan∠CDF的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为___.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△BOD都是等腰直角三角形,∠ACB=∠BDO=90°,且点A在反比例函数
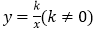 的图象上,若
的图象上,若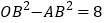 ,则k的值为 ____.
,则k的值为 ____. 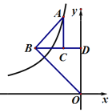
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A做AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;若AC=4,AB=5,求菱形ADCF的面积.
(3)当△ABC满足什么条件时,四边形ADCF是正方形,请说明理由.
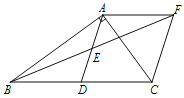
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m,同时测量出DE在阳光下的投影长为6m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)请你计算DE的长.
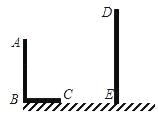
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在由边长为1的小正方形组成的网格图中有△ABC,建立平面直角坐标系后,点O的坐标是(0,0).
(1)以O为位似中心,作△A′B′C′∽△ABC,△A′B′C′与△ABC相似比为2:1,且△A′B′C′在第二象限;
(2)在上面所画的图形中,若线段AC上有一点D,它的横坐标为k,点D在A′C′上的对应点D′的横坐标为﹣2﹣k,则k= .
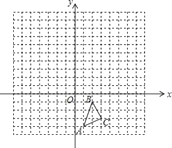
相关试题

