搜索
【题目】如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，CD于点E，F，连接PB，PD.若AE＝2，PF＝8.则图中阴影部分的面积为___．
参考答案：
【答案】16
【解析】
作PM⊥AD于M，交BC于N，则有四边形AEPM、四边形DFPM、四边形CFPN、四边形BEPN都是矩形，可得S△PEB=S△PFD＝8，则可得出S阴．
作PM⊥AD于M，交BC于N，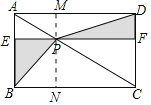
则有四边形AEPM、四边形DFPM、四边形CFPN、四边形BEPN都是矩形，
∴S△ADC=S△ABC，S△AMP=S△AEP，S△PBE=S△PBN，S△PFD=S△PDM，S△PFC=S△PCN，
∴S△DFP=S△PBE=
×2×8=8，
∴S阴=8+8=16.
故答案是：16．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知菱形的一个角与三角形的一个角重合，然后它的对角顶点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图，在△CFE中，CF=6，CE=12，∠FCE=45°，以点C为圆心，以任意长为半径作AD，再分别以点A和点D为圆心，大于
AD长为半径做弧，交EF于点B，AB∥CD.
（1）求证：四边形ACDB为△CFE的亲密菱形；
（2）求四边形ACDB的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线
分别与x轴、y轴交于
两点，与直线
交于点C（4，2）．（1）点A坐标为（ ， ），B为（ ， ）；
（2）在线段
上有一点E，过点E作y轴的平行线交直线
于点F，设点E的横坐标为m，当m为何值时，四边形
是平行四边形；（3）若点P为x轴上一点，则在平面直角坐标系中是否存在一点Q，使得
四个点能构成一个菱形．若存在，求出所有符合条件的Q点坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，BC切⊙O于点B，连接CO并延长交⊙O于点D、E，连接AD并延长交BC于点F．
（1）试判断∠CBD与∠CEB是否相等，并证明你的结论；
（2）求证：
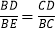；（3）若BC=
AB，求tan∠CDF的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC和△BOD都是等腰直角三角形，∠ACB=∠BDO=90°，且点A在反比例函数
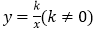的图象上，若
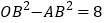，则k的值为 ____. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线
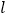∥AB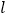，与 AB 之间的距离为 2 ，C、D 是直线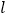上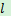
两个动点（点 C在 D 点的左侧），且 AB=CD=5．连接 AC、BC、BD，将△ABC 沿 BC 折叠得到△A′BC．若以 A′、C、B、D 为顶点的四边形为矩形，则此矩形相邻两边之和为____．
-
科目： 来源： 题型：
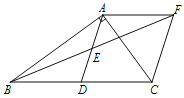
查看答案和解析>>【题目】已知：在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点．过点A做AF∥BC交BE的延长线于点F．
（1）求证：△AEF≌△DEB；
（2）证明四边形ADCF是菱形；若AC=4，AB=5，求菱形ADCF的面积．
（3）当△ABC满足什么条件时，四边形ADCF是正方形，请说明理由.
相关试题
