【题目】如图,在△ABC与△ADE中,∠BAC=∠DAE=90°,AD=AE,AB=AC,且B、D、E三点在一条直线上.
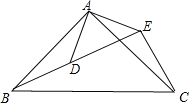
(1)求证:BD=CE.
(2)求∠BEC的度数.
(3)写出BE与AE、CE的数量关系是 .
参考答案:
【答案】(1)见解析;(2)∠BEC=90°;(3)结论:BE=CE+![]() AE.理由见解析.
AE.理由见解析.
【解析】
(1)欲证明BD=CE,只要证明△ABD≌△ACE即可;
(2)利用全等三角形的性质可得∠AEC=∠ADB=135°,即可解决问题;
(3)结论:BE=EC+![]() AE.利用全等三角形的性质以及等腰直角三角形的性质即可证明.
AE.利用全等三角形的性质以及等腰直角三角形的性质即可证明.
(1)证明:∠BAC=∠DAE=90°
∴∠BAD=∠CAE,
∵AB=AC,AD=AE
∴△ABD≌△ACE,
∴BD=CE.
(2)解:∵△ABD≌△ACE,
∴∠ADB=∠AEC,
又∵∠ADB=∠DAE+∠AED=135°,
∴∠AEC=∠AED+∠BEC=135°,
∴135°=45°+∠BEC
∴∠BEC=90°.
③解:结论:BE=CE+![]() AE.
AE.
理由:∵△ABD≌△ACE,
∴BD=CE,
∵△ADE是等腰直角三角形,
∴DE=![]() AE,
AE,
∴BE=BD+DE=CE+![]() AE.
AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】贵州省是我国首个大数据综合试验区,大数据在推动经济发展、改善公共服务等方面日益显示出巨大的价值,为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:

(1)本次参与调查的人数有 人;
(2)关注城市医疗信息的有 人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是 度;
(4)说一条你从统计图中获取的信息.
-
科目: 来源: 题型:
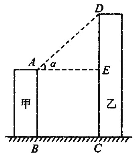
查看答案和解析>>【题目】如图所示.线段AB、DC分别表示甲、乙两座建筑物的高.AB⊥BC,DC⊥BC,两建筑物间距离BC=30米,若甲建筑物高AB=28米,在A点测得D点的仰角α=45°,则乙建筑物高DC=______米.
-
科目: 来源: 题型:
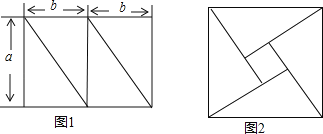
查看答案和解析>>【题目】已知将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图1,再用这四个三角形拼成如图2所示的正方形,中间形成一个正方形的空洞.经测量得长方形的面积为24,正方形的边长为5.试通过你获取的信息,求a2+b2和a2﹣b2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知△ABC为等边三角形,动点D在边AC上,动点P在边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连结AP、BD交于Q,两点运动的过程中,AP=BD成立吗?请证明你的结论.
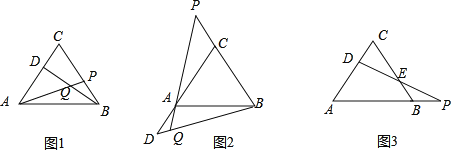
(2)如果把原题中的“动点D在边AC上,动点P在边BC上,”改为:“动点D在射线CA上、动点P在射线BC上运动,”其他条件不变,如图2所示,AP=BD还成立吗?说明理由,并求出∠BQP的大小.
(3)如果把原题中的“动点P在边BC上”,改为“动点P在射线AB上运动”,连结DP交BC于E,其他条件不变,如图3,则动点D、P在运动过程中,请你写出DE与PE的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形一腰上的高与另一腰的夹角是45°,则底角的度数为( )
A.67°50'B.67.5°C.22.5°D.22.5°或67.5°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的有( ).
①已知任意一边和一个锐角对应相等的两个直角三角形全等.
②任意两角和一边对应相等的两个三角形全等.
③已知任意两边和一角对应相等的两个三角形全等.
④已知腰和顶角对应相等的两个等腰三角形全等.
⑤如果两个三角形有两条边及其中一边上的中线分别相等,那么这两个三角形全等.
A.1个B.2个C.3个D.4个
相关试题

