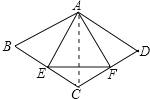
【题目】如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连结AE、EF、AF,则△AEF的周长为( )

A. 2![]() cm B. 4
cm B. 4![]() cm C. 3
cm C. 3![]() cm D. 3cm
cm D. 3cm
参考答案:
【答案】C
【解析】
首先根据菱形的性质证明△ABE≌△ADF,然后连接AC可推出△ABC以及△ACD为等边三角形.根据等腰三角形三线合一的定理又可推出△AEF是等边三角形.根据勾股定理可求出AE的长继而求出周长.
解:∵四边形ABCD是菱形,
∴AB=AD=BC=CD,∠B=∠D,
∵E、F分别是BC、CD的中点,
∴BE=DF,
在△ABE和△ADF中,
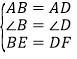
∴△ABE≌△ADF(SAS),
∴AE=AF,∠BAE=∠DAF.
连接AC,
∵∠B=∠D=60°,
∴△ABC与△ACD是等边三角形,
∴AE⊥BC,AF⊥CD(等腰三角形底边上的中线与底边上的高线重合),
∴∠BAE=∠DAF=30°,
∴∠EAF=60°,
∴△AEF是等边三角形.
![]() AE=
AE=![]() cm,
cm,
![]() 周长是3
周长是3![]() cm,
cm,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)4x=5x﹣5
(2)4x+3(2x﹣3)=12﹣(x﹣4)
(3)
 .
.(4)
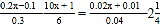
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,D为AB的中点,点P在线段上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动.当△BPD与△CQP全等时,求点P运动的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°。

①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?写出你猜想的结论,并说明理由;
②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数量关系和位置关系?请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某酒店有三人间、双人间客房若干,各种房型每天的收费标准如下:
普通(元/间)
豪华(元/间)
三人间
160
400
双人间
140
300
一个50人的旅游团到该酒店入住,选择了一些三人普通间和双人豪华间入住,且恰好住满.已知该旅游团当日住宿费用共计4020元,问该旅游团入住的三人普通间和双人豪华间各为几间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一面积为5
 的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 .
的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】小彬和小明每天早晨坚持跑步,小彬每秒跑4米,小明每秒跑6米.
(1)如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?
(2)如果小明站在百米跑道的起点处,小彬站在他前面10米处,两人同时同向起跑,几秒后小明能追上小彬?
(2)如果他们都站在四百米环形跑道的起点处,两人同时同向起跑,几分钟后他们再次相遇?
相关试题

