【题目】已知:如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.
(1)BE与DF是否相等?请说明理由;
(2)若AB=14,AD=6,求DF的长.

参考答案:
【答案】(1)BE=DF,理由见解析;(2)4.
【解析】
(1)由角平分线的性质可得CF=CE,然后可用HL判定Rt△CDF≌Rt△CBE,所以BE=DF;
(2)先证明Rt△ACE≌Rt△ACF得到AF=AE,然后由线段关系可求出DF.
证明:(1)BE=DF,
理由如下:
∵AC平分∠BAD,
且CE⊥AB于E,CF⊥AD于F,
∴CF=CE,∠CFD=∠CEB=90°,
在Rt△CDF和Rt△CBE中,
![]()
∴Rt△CDF≌Rt△CBE(HL)
∴BE=DF
(2)∵CE=CF,AC=AC,
∴Rt△ACE≌Rt△ACF(HL)
∴AF=AE,
∵AB=AE+BE=AF+DF=14①,AD=AF﹣DF=6②,
∴①﹣②可得DF=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 边长为
边长为 ,
, 轴,
轴, 轴,顶点
轴,顶点 恰好落在双曲线
恰好落在双曲线 上,边
上,边 、
、 分别交双曲线于点
分别交双曲线于点 、
、 ,若线段
,若线段 过原点,则
过原点,则 的面积为( )
的面积为( )
A. 1 B.
 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的二次函数
的二次函数 与
与 ,这两个二次函数的图象中的一条与
,这两个二次函数的图象中的一条与 轴交于
轴交于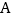 ,
, 两个不同的点.
两个不同的点. 试判断哪个二次函数的图象经过
试判断哪个二次函数的图象经过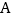 ,
, 两点;
两点; 若
若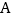 点坐标为
点坐标为 ,试求
,试求 点坐标;
点坐标; 在
在 的条件下,对于经过
的条件下,对于经过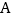 ,
, 两点的二次函数,当
两点的二次函数,当 取何值时,
取何值时, 的值随
的值随 值的增大而减小.
值的增大而减小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在四边形ABCD中,∠A=90°.若AB=4cm,AD=3cm,CD=12cm,BC=13cm,
(1)请说明BD⊥CD;
(2)求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,
中, ,
, ,
, .长为
.长为 的线段
的线段 在
在 的边
的边 上沿
上沿 方向以
方向以 的速度向点
的速度向点 运动(运动前点
运动(运动前点 与点
与点 重合).过
重合).过 ,
, 分别作
分别作 的垂线交直角边于
的垂线交直角边于 ,
, 两点,线段
两点,线段 运动的时间为
运动的时间为 .
. 若
若 的面积为
的面积为 ,写出
,写出 与
与 的函数关系式(写出自变量
的函数关系式(写出自变量 的取值范围);
的取值范围); 线段
线段 运动过程中,四边形
运动过程中,四边形 有可能成为矩形吗?若有可能,求出此时t的值;若不可能,说明理由;
有可能成为矩形吗?若有可能,求出此时t的值;若不可能,说明理由;
 为何值时,以
为何值时,以 ,
, ,
, 为顶点的三角形与
为顶点的三角形与 相似?
相似? -
科目: 来源: 题型:
查看答案和解析>>【题目】善于不断改进学习方法的小迪发现,对解题进行回顾反思,学习效果更好.某一天小迪有20分钟时间可用于学习.假设小迪用于解题的时间
 (单位:分钟)与学习收益量
(单位:分钟)与学习收益量 的关系如图1所示,用于回顾反思的时间
的关系如图1所示,用于回顾反思的时间 (单位:分钟)与学习收益
(单位:分钟)与学习收益 的关系如图2所示(其中
的关系如图2所示(其中 是抛物线的一部分,
是抛物线的一部分, 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.(1)求小迪解题的学习收益量
 与用于解题的时间
与用于解题的时间 之间的函数关系式;
之间的函数关系式;(2)求小迪回顾反思的学习收益量
 与用于回顾反思的时间
与用于回顾反思的时间 的函数关系式;
的函数关系式;(3)问小迪如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题:如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D为BC边上一点(不与点B,C重合)将线段AD绕点A逆时针旋转90°得到AE,连接EC.求证:△ABD≌△ACE;
(2)探索:如图2,在Rt△ABC与Rt△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段BD2、CD2、DE2之间满足的等量关系,并证明你的结论;
(3)应用:如图3,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=6,CD=2,求AD的长.

相关试题

