【题目】为了改善教室空气环境,某校九年级1班班委会计划到朝阳花卉基地购买绿植.已知该基地一盆绿萝与一盆吊兰的价格之和是12元.班委会决定用60元购买绿萝,用90元购买吊兰,所购绿萝数量正好是吊兰数量的两倍.
(1)分别求出每盆绿萝和每盆吊兰的价格;
(2)该校九年级所有班级准备一起到该基地购买绿萝和吊兰共计90盆,其中绿萝数量不超过吊兰数量的一半,该基地特地对吊兰价格给出了如下的优惠政策,一次性购买的吊兰超过20盆时,超过部分的吊兰每盆的价格打8折,根据该基地的优惠信息,九年级购买这两种绿植各多少盆时总费用最少?最少费用是多少元?
参考答案:
【答案】(1)每盆绿萝是3元,每盆吊兰9元;(2)购买吊兰60盆,绿萝30盆时,总费用最少,为558元.
【解析】试题分析:(1)设每盆绿萝x元,则每盆吊兰(12﹣x)元,根据所购绿萝数量正好是吊兰数量的两倍,列出方程,求解即可;
(2)设购买吊兰x盆,总费用y元,根据购买绿萝和吊兰共计90盆,其中绿萝数量不超过吊兰数量的一半,列出不等式,求出x的取值范围,再表示出总费用,然后根据函数性,即可得出答案.
试题解析:解:(1)设每盆绿萝x元,则每盆吊兰(12﹣x)元,根据题意得:
![]() =
=![]() ×2
×2
解得:x=3,经检验x=3是方程的解,则12﹣x=12﹣3=9(元).
答:每盆绿萝是3元,每盆吊兰9元;
(2)设购买吊兰x盆,总费用y元,根据题意得:
90﹣x≤![]() x
x
解得:x≥60,则y=20×9+9×0.8(x﹣20)+3(90﹣x)=4.2x+306.
∵4.2>0,∴y随x的增大而增大,∴当x=60时,y取得最小值,最小值为4.2×60+306=558,∴购买吊兰60盆,绿萝30盆时,总费用最少,为558元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点0为直线AB上一点,∠AOC=50
 ,OD平分∠AOC,∠DOE=90
,OD平分∠AOC,∠DOE=90 .
.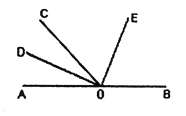
(1)请你数一数,图中有多少个小于平角的角:
(2)求出∠BOD的度数;
(3)试判断OE是否平分∠BOC,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=8,DH=2,平移距离为3,则阴影部分的面积是_____.
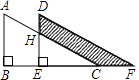
-
科目: 来源: 题型:
查看答案和解析>>【题目】①将下列各数填入相应的括号中:
0,-2019,7.01,+6,+30﹪,
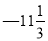
负数:{ }
正数:{ }
整数:{ }
②.画一条数轴,在数轴上标出以下各点,然后用“<”符号连起来.
-
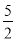 ;-(-4);-|-1|;
;-(-4);-|-1|;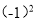 ;0;
;0;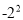 ;2.5;
;2.5; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是最大的负整数,b、c满足
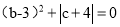 ,且a,b,c分别是点A,B,C在数轴上对应的数.
,且a,b,c分别是点A,B,C在数轴上对应的数.(1)求a,b,c的值,并在数轴上标出点A,B,C;
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
-
科目: 来源: 题型:
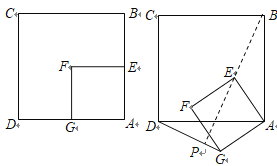
查看答案和解析>>【题目】如图,正方形ABCD和正方形AEFG,边AE在边AB上,AB=2AE=2.将正方形AEFG绕点A逆时针旋转60°,BE的延长线交直线DG于点P ,旋转过程中点P运动的路线长为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“滴滴快车”是一种便捷的出行工具,计价规则如下表:
计费项目
里程费
时长费
单价
1.4元/千米
0.5元/分钟
注:车费由里程费、时长费两部分构成,其中里程费按行车的实际里程计费,时长费按行车的实际时间计算。车费不足8元的按最低消费8元收取。为了推广和扩大“滴滴快车”的市场占有率,公司近期推出优惠政策,凡车费满10元,将给予8折优惠。
随着互联网的不断发展,更多的人们选择了“滴滴快车”出行。假设“滴滴快车”的平均行车速度为50 km/h,请回答下列问题:
(1)小明和小冰各自乘坐“滴滴快车”,行车里程分别为3千米和10千米,请问他们各自需付车费多少钱?
(2)张老师与王老师的家和学校在同一条直线上,位置如图所示.一天,张老师和王老师各自从学校“滴滴快车”回家,分别付车费9.6元和24元.请问,张老师和王老师的家相距多少千米?

相关试题

