【题目】“滴滴快车”是一种便捷的出行工具,计价规则如下表:
计费项目 | 里程费 | 时长费 |
单价 | 1.4元/千米 | 0.5元/分钟 |
注:车费由里程费、时长费两部分构成,其中里程费按行车的实际里程计费,时长费按行车的实际时间计算。车费不足8元的按最低消费8元收取。为了推广和扩大“滴滴快车”的市场占有率,公司近期推出优惠政策,凡车费满10元,将给予8折优惠。 | ||
随着互联网的不断发展,更多的人们选择了“滴滴快车”出行。假设“滴滴快车”的平均行车速度为50 km/h,请回答下列问题:
(1)小明和小冰各自乘坐“滴滴快车”,行车里程分别为3千米和10千米,请问他们各自需付车费多少钱?
(2)张老师与王老师的家和学校在同一条直线上,位置如图所示.一天,张老师和王老师各自从学校“滴滴快车”回家,分别付车费9.6元和24元.请问,张老师和王老师的家相距多少千米?
![]()
参考答案:
【答案】(1)小明需付车费8元,小冰需付车费16元;(2)张老师和王老师家相距19.8千米或21千米.
【解析】试题分析:(1)首先明确收费标准分两种情况:①8元以下,按最低消费8元收取;②凡车费满10元,将给予8折优惠,收费分两部分,里程费和时长费;
(1):小明:6元<8元,按8元收费;
小冰:20元>16元,按8折收费;
(2):设张老师家距离学校x千米,王老师家距离学校y千米,由于张老师付的车费9.6元<10元,故分两种情况:①原车费未满10元,②原车费满10元打8折,由此得出方程分别求x、y的值,再计算x+y即可.
试题解析:(1)小明: ![]() 元,
元,
![]() 6元<8元,
6元<8元,
![]() 小明需付车费8元;
小明需付车费8元;
小冰: ![]() 元,
元,
![]() 元,
元,
![]() 小冰需付车费16元,
小冰需付车费16元,
答:小明需付车费8元,小冰需付车费16元.
(2)设张老师家距离学校x千米,王老师家距离学校y千米。
张老师:①原车费未满10元时: ![]()
解得: ![]() ;
;
②原车费满10元打8折时: ![]() ,
,
解得: ![]() ,
,
![]() 张老师家距离学校4.8千米或6千米,
张老师家距离学校4.8千米或6千米,
王老师: ![]() ,
,
解得![]() ,
,
![]() 张老师家距离学校15千米,
张老师家距离学校15千米,
4.8+15=19.8千米,6+15=21千米,
答:张老师和王老师家相距19.8千米或21千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:2(3a2b﹣ab2+1)﹣(a2b﹣2ab2),其中a=﹣2,b=﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了实现街巷硬化工程高质量“全覆盖”,我省今年1﹣4月公路建设累计投资92.7亿元,该数据用科学记数法可表示为( )
A.0.927×1010
B.92.7×1010
C.9.27×1011
D.9.27×109 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形的两条对角线的一个交角为60°,两条对角线的长度的和为20cm,则这个矩形的一条较短边的长度为( )
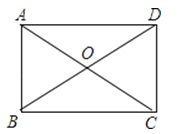
A.10cm
B.8cm
C.6cm
D.5cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知数轴上两点A、B对应的数分别为﹣2、5,点P为数轴上的一动点,其对应的数为x.
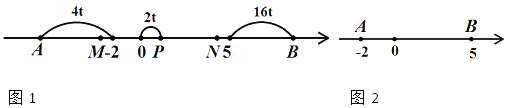
(1)PA= ;PB= (用含x的式子表示)
(2)在数轴上是否存在点P,使PA+PB=10?若存在,请直接写出x的值;若不存在,请说明理由.
(3)如图2,点P以2个单位/s的速度从点O向右运动,同时点A以4个单位/s的速度向左运动,点B以16个单位/s的速度向右运动,在运动过程中,M、N分别是AP、OB的中点,问:
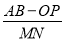 的值是否发生变化?请说明理由.
的值是否发生变化?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上A,B表示的数分别是3和﹣5,它们之间的距离可以表示为( )
A. ﹣5+3B. ﹣5﹣3C. |﹣5+3|D. |﹣5﹣3|
-
科目: 来源: 题型:
查看答案和解析>>【题目】若方程2x+1=﹣3的解是关于x的方程7﹣2(x﹣a)=3的解,则a的值为( )
A. ﹣2B. ﹣4C. ﹣5D. ﹣6
相关试题

