搜索
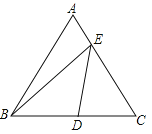
【题目】（2015攀枝花，第15题，4分）如图，在边长为2的等边△ABC中，D为BC的中点，E是AC边上一点，则BE+DE的最小值为_____．
参考答案：
【答案】
．
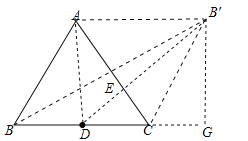
【解析】试题作B关于AC的对称点B′，连接BB′、B′D，交AC于E，此时BE+ED=B′E+ED=B′D，根据两点之间线段最短可知B′D就是BE+ED的最小值，∵B、B′关于AC的对称，∴AC、BB′互相垂直平分，∴四边形ABCB′是平行四边形，∵三角形ABC是边长为2，∵D为BC的中点，∴AD⊥BC，∴AD=
，BD=CD=1，BB′=2AD=
，作B′G⊥BC的延长线于G，∴B′G=AD=，
在Rt△B′BG中，BG=
=
=3，∴DG=BG﹣BD=3﹣1=2，
在Rt△B′DG中，BD=
=
=．故BE+ED的最小值为．
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的一元二次方程x2﹣3x﹣k=0有两个不相等的实数根．
（1）求k的取值范围；
（2）请选择一个k的负整数值，并求出方程的根． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=5，BC=3，则BD的长为（ ）
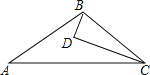
A. 1 B. 1.5 C. 2.5 D. 4
-
科目： 来源： 题型：
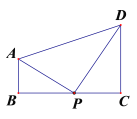
查看答案和解析>>【题目】如图，AB⊥BC，DC⊥BC，AB=1，DC=2，BC=3，点 P 是线段 BC 上一动点（不与点 B，C 重合），若△APD 是等腰三角形，则 CP 的长是_______________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c经过A（﹣1，0）、B（3，0）、C（0，3）三点，直线l是抛物线的对称轴．
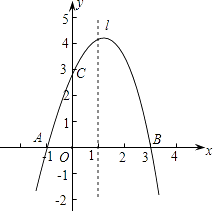
（1）求抛物线的函数关系式；
（2）设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；
（3）在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．
（4）若抛物线顶点为D，点Q为直线AC上一动点，当△DOQ的周长最小时，求点Q的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=ax2+bx+c（a≠0）的图象如图，结论：①ac＜0；②a﹣b+c＜0；③b2﹣4ac≥0；④y随x的增大而增大，其中正确的个数（ ）
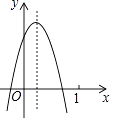
A.4个
B.3个
C.2个
D.1个 -
科目： 来源： 题型：
查看答案和解析>>【题目】在同一直角坐标系中，函数y=mx+m和y=﹣mx2+2x+2（m是常数，且m≠0）的图象可能是（ ）
A.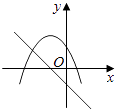
B.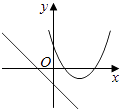
C.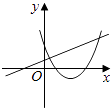
D.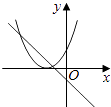
相关试题
