【题目】已知抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次函数y2= ![]() x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.
x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.
参考答案:
【答案】解:根据OC长为8可得一次函数中的n的值为8或﹣8. 分类讨论:①n=8时,易得A(﹣6,0)如图1,
∵抛物线经过点A、C,且与x轴交点A、B在原点的两侧,
∴抛物线开口向下,则a<0,
∵AB=16,且A(﹣6,0),
∴B(10,0),而A、B关于对称轴对称,
∴对称轴直线x= ![]() =2,
=2,
要使y1随着x的增大而减小,且a<0,
∴x≥2;
②n=﹣8时,易得A(6,0),如图2,
∵抛物线过A、C两点,且与x轴交点A,B在对称轴两侧,
∴抛物线开口向上,则a>0,
∵AB=16,且A(6,0),
∴B(﹣10,0),而A、B关于对称轴对称,
∴对称轴直线x= ![]() =﹣2,
=﹣2,
要使y1随着x的增大而减小,且a>0,
∴x≤﹣2.
综上所述,x≥2或x≤﹣2.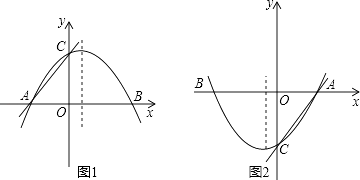
【解析】根据OC的长度确定出n的值为8或﹣8,然后分①n=8时求出点A的坐标,然后确定抛物线开口方向向下并求出点B的坐标,再求出抛物线的对称轴解析式,然后根据二次函数的增减性求出x的取值范围;②n=﹣8时求出点A的坐标,然后确定抛物线开口方向向上并求出点B的坐标,再求出抛物线的对称轴解析式,然后根据二次函数的增减性求出x的取值范围.
【考点精析】关于本题考查的二次函数的性质和抛物线与坐标轴的交点,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AB∥DC,线段AG,BG分别交CD于点E,F,DE=CF. 求证:△GAB是等腰三角形.

-
科目: 来源: 题型:
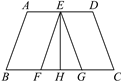
查看答案和解析>>【题目】如图所示,已知AD∥BC,AB∥EF,CD∥EG,且点E在直线AD上,点F,H,G在直线BC上,EH平分∠FEG,∠A=∠D=110°,线段EH的长是不是两条平行线AD,BC之间的距离?为什么?
-
科目: 来源: 题型:
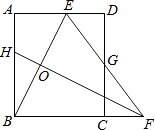
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )

A. 点A B. 点B
C. A,B之间 D. B,C之间
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有50位学生,每位学生都有一个序号,将50张编有学生序号(从1号到50号)的卡片(除序号不同外其它均相同)打乱顺序重新排列,从中任意抽取1张卡片.
(1)在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),求取到的卡片上序号是20的倍数或能整除20的概率;
(2)若规定:取到的卡片上序号是k(k是满足1≤k≤50的整数),则序号是k的倍数或能整除k(不重复计数)的学生能参加某项活动,这一规定是否公平?请说明理由;
(3)请你设计一个规定,能公平地选出10位学生参加某项活动,并说明你的规定是符合要求的. -
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)先求解下列两题: ①如图①,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数;
②如图②,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数 的图象经过点B,D,求k的值.
的图象经过点B,D,求k的值.
(2)解题后,你发现以上两小题有什么共同点?请简单地写出.
相关试题

