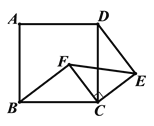
【题目】如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF, BC=5,CF=3,BF=4.
求证:DE∥FC
参考答案:
【答案】证明见解析.
【解析】试题分析:根据正方形以及△ECF的性质得出△BCF和△DCE全等,从而得出∠DEC=∠BFC,根据BC、CF和BF的长度得出∠BFC=90°,即∠DEC=90°,最后根据同旁内角互补两直线平行得出答案.
试题解析:∵四边形 ABCD是正方形 ∴∠BCF+∠FCD=90°,BC=CD,
∵△ECF是等腰直角三角形, ∴∠ECD+∠FCD=90°, CF=CE,
∴∠BCF=∠ECD, ∴△BCF≌△DCE,
在△BFC中,BC=5,CF=3,BF=4, ∴ CF2+BF2=BC2 ∴∠BFC=90°,
∵△BCF≌△DCE,∴DE=BF=4,∠BFC=∠DEC=∠FCE=90°,∴DE∥FC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:2(x2y+3xy2)﹣[﹣2(x2y+4)+xy2]﹣3xy2,其中x=2,y=﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC,
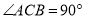 中,D是BC的中点,DE⊥BC,CE∥AD,若
中,D是BC的中点,DE⊥BC,CE∥AD,若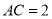 ,
, 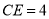 ,求四边形ACEB的周长.
,求四边形ACEB的周长.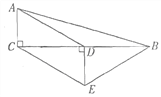
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=40°,AB的垂直平分线MN交AC于点D,∠DBC=30°,若AB=m,BC=n,则△DBC的周长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将△ABC沿着某一方向平移一定的距离得到△MNL,则下列结论中正确的有( )
①AM∥BN;②AM=BN;③BC=ML;④∠ACB=∠MNL。

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,试判断BE与CF的位置关系,并说明你的理由.请补全下列说理过程.
,试判断BE与CF的位置关系,并说明你的理由.请补全下列说理过程.
解:BE ______ CF.
理由是:
 已知
已知 .
. ______
______  ______
______  垂直的定义
垂直的定义
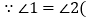 已知
已知 .
. =______
=______  .(等式的基本性质)
.(等式的基本性质)即
 ______
______  ______
______  ( ______________________
( ______________________ 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F分别是AB、BC上的点,且AE=BF.求证:CE=DF.

相关试题

