【题目】探究思考:(本题直接填空,不必写出解题过程)
问题:在数轴上,点A表示的数为![]() ,则到点A的距离等于3的点所表示的数是 ;
,则到点A的距离等于3的点所表示的数是 ;
变式思考一:如图1,在数轴上有六个点A、B、C、D、E、F,且相邻两点间距离相等,若点A表示的数是![]() ,点F表示的数为11,则与点C表示的数最近的整数是 ;
,点F表示的数为11,则与点C表示的数最近的整数是 ;
![]()
变式思考二:已知数轴上有A、B、C三点,分别代表![]() ,电子蚂蚁从A向点C方向以4个单位/秒的速度爬行.则爬行到 秒时,电子蚂蚁到A、B、C的距离和为40个单位.
,电子蚂蚁从A向点C方向以4个单位/秒的速度爬行.则爬行到 秒时,电子蚂蚁到A、B、C的距离和为40个单位.
参考答案:
【答案】问题:-4或2;变式思考一:1;变式思考二:2或5
【解析】
问题:数轴上若点A表示的数是-1,另一点与点A的距离为3,则分这点在点A的左边和右边两种情况讨论可得;
变式思考一:先求出相邻两个字母的间距,然后求到点C表示的数,即可得到距离C最近的整数;
变式思考二:设y秒后甲到A,B,C三点的距离之和为40个单位,分电子蚂蚁应位于AB或BC之间两种情况讨论即可求解.
解:问题:分两种情况:①这个点在A左边时,这个点表示的数是-1-3=-4;②这个点在A右边时,这个点表示的数是-1+3=2;
故答案为:-4或2;
变式思考一:相邻两个字母的间距=[11-(-5)]÷5=3.2,所以点C表示的数=-5+3.2×2=1.4,
则与点C表示的数最近的整数是1,
故答案为:1;
变式思考二:设y秒后甲到A,B,C三点的距离之和为40个单位,
B点距A,C两点的距离为14+20=34<40,A点距B、C两点的距离为14+34=48>40,C点距A、B的距离为34+20=54>40,故甲应为于AB或BC之间.
①AB之间时:4y+(14-4y)+(14-4y+20)=40
解得y=2;
②BC之间时:4y+(4y-14)+(34-4y)=40,
解得y=5.
故答案为:2或5;
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
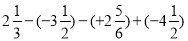 ;
;(2)
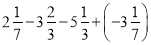 ;
;(3)
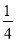 +(-
+(-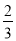 )+
)+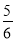 +(-
+(-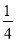 )+ (-
)+ (-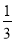 );
);(4)5.6+(-0.9)+4.4+(-8.1)+(-1);
(5)(-3
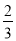 )-(-1
)-(-1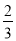 )-(-2
)-(-2 )+(-1.75);
)+(-1.75);(6)-108-(-112)+23+18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)

(2)(-2
 )+(-1
)+(-1 )-(-2
)-(-2 )-(-4
)-(-4 )
)(3)(
 —
— +
+ )
)
(4)
 ×0.125×
×0.125× ×
×
(5)

(6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面文字:
对于(﹣5
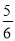 )+(﹣9
)+(﹣9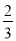 )+17
)+17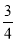 +(﹣3
+(﹣3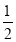 )
)可以如下计算:
原式=[(﹣5)+(﹣
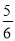 )]+[(﹣9)+(﹣
)]+[(﹣9)+(﹣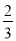 )]+(17+
)]+(17+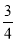 )+[(﹣3)+(﹣
)+[(﹣3)+(﹣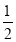 )]
)]=[(一5)+(﹣9)+17+(一3)]+[(﹣
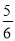 )+(﹣
)+(﹣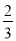 )+
)+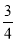 +(﹣
+(﹣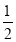 )]=0+(﹣1
)]=0+(﹣1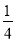 )
)=﹣1
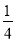
上面这种方法叫拆项法,你看懂了吗?
仿照上面的方法,请你计算:(﹣1
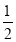 )+(﹣2000
)+(﹣2000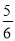 )+4000
)+4000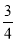 +(﹣1999
+(﹣1999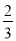 )
) -
科目: 来源: 题型:
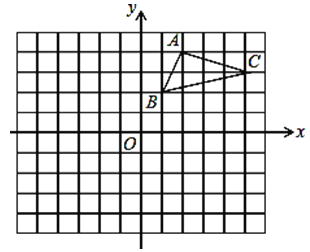
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4)
(1)画出△ABC先向左平移1个单位,再向下平移4个单位得到的△A1B1C1,写出点A1的坐标____________
(2)画出△A1B1C1绕原点O顺时针旋转90°,得到△A2B2C2,写出点A2的坐标_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.

(1)在图中画出点B,并求出B处与灯塔P的距离(结果取整数);
(2)用方向和距离描述灯塔P相对于B处的位置.
(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan53°≈1.33,
 ≈1.41)
≈1.41) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ADE中,点E在BC边上,∠B=∠D,AB=AD,∠BAD=∠CAE,
(1)求证:AE=AC
(2)若∠AEC=60°,将△ADE绕点A逆时针旋转后与△ABC重合,则这个旋转角的度数__
(3)若AC=4,BC=7,∠AEC=60°,求△ABE的面积.

相关试题

