【题目】如图,在平行四边形ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N.给出下列结论:①△ABM≌△CDN;②AM=![]() AC;③DN=2NF;④S△AMB=
AC;③DN=2NF;④S△AMB=![]() △ABC;其中正确的结论是______________(只填序号)。
△ABC;其中正确的结论是______________(只填序号)。

参考答案:
【答案】①②③.
【解析】
本题先结合平行四边形性质,根据ASA得出△ABM≌△CDN,从而得出DN=BM,AM=CN;再由三角形中位线得出CN=MN,BM=DN=2NF,同时S![]() =
=![]() S
S![]() .
.
∵因为平行四边形ABCD,
∴AD=BC,AB=CD,且AD∥BC,AB∥CD∠BAE=∠DCF,
∵E、F分别是边AD、BC的中点,
∴AE=DE=BF=CF,
∴四边形BFDE是平行四边形
∴BE∥DF,
在△ABE和△CDF中
∵ ,
,
∴△ABE≌△CDF(SAS),
∴∠ABM=∠CDN,
∵AB∥CD,
∴∠BAM=∠DCN,
在△ABM和△CDN中
∵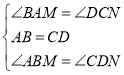 ,
,
∴△ABM≌△CDN(ASA),∴①正确;
∵E是AD的中点,BE∥DF,
∴M是AN的中点,
同理N是CM的中点,
∴AM=![]() AC,故②正确;
AC,故②正确;
∵F为BC的中点,
∴NF为三角形BCM的中位线,
∴BM=2NF
∴DN=2NF,故③正确;
∵CN=MN=AM,
∴S![]() =
=![]() S
S![]() ,故④不正确,
,故④不正确,
∴其中正确的结论是①②③.
故答案为:①②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是△ABC的外心,I是△ABC的内心,连AI并延长交BC和⊙O于D、E两点.
(1)求证:EB=EI;
(2)若AB=4,AC=3,BE=2,求AI的长.

-
科目: 来源: 题型:
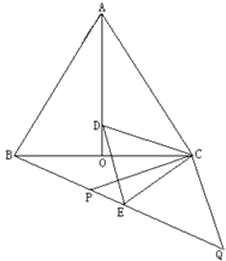
查看答案和解析>>【题目】如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE;
(2)延长BE至Q,P为BQ上一点,连接CP、CQ使CP=CQ=5,若BC=8时,求PQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线y=-
 x2 +bx+c交y轴于点C(0,2),经过点Q(2,2).直线y=x+4分别交x轴、y轴于点B、A.
x2 +bx+c交y轴于点C(0,2),经过点Q(2,2).直线y=x+4分别交x轴、y轴于点B、A.(1)直接填写抛物线的解析式________;
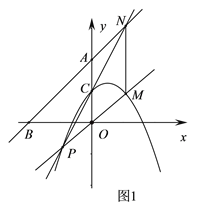
(2)如图1,点P为抛物线上一动点(不与点C重合),PO交抛物线于M,PC交AB于N,连MN.
求证:MN∥y轴;
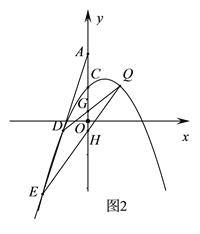
(3)如图,2,过点A的直线交抛物线于D、E,QD、QE分别交y轴于G、H.求证:CG CH为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形的一个内角平分线把矩形的一条边分成长为3和5两部分,则该矩形的面积是__。
-
科目: 来源: 题型:
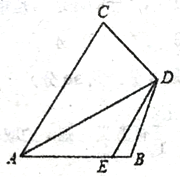
查看答案和解析>>【题目】如图:四边形ABDC中,CD=BD,E为AB上一点,连接DE,且∠CDE=∠B.若∠CAD=∠BAD=30°,AC=5,AB=3,则EB=______________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产480个零件.当生产任务完成一半时,停止生产进行反思和改进,用时20分钟.恢复生产后工作效率比原来可以提高20%,要求比原计划提前40分钟完成任务,那么反思改进后每小时需要生产多少个零件?
相关试题