【题目】如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx﹣2的图象经过点A、C,并与y轴交于点E,反比例函数y= ![]() 的图象经过点A.
的图象经过点A.
(1)点E的坐标是;
(2)求反比例函数的解析式;
(3)求当一次函数的值小于反比例函数的值时,x的取值范围.
参考答案:
【答案】
(1)E(0,﹣2)
(2)解:把C(4,0)代入y=kx﹣2得4k﹣2=0,解得k= ![]() ,
,
∴一次函数解析式为y= ![]() x﹣2;
x﹣2;
∵OC=4,
∴A点坐标为(6,1),
把A(6,1)代入y= ![]() 得m=6×1=6,
得m=6×1=6,
∴反比例函数解析式为y= ![]()
(3)解:令 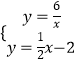
解得 ![]() ,
,
∴另一个交点(﹣2,﹣3),
∴观察图象得:当x<﹣2或 0<x<6时次函数的值小于反比例函数的值
【解析】解:(1)一次函数y=kx﹣2中令x=0得y=﹣2,
所以E(0,﹣2);
(1)把x=0代入求出y的值,即可得E的坐标;
(2)利用待定系数法求出一次函数解析式,从而求出A的坐标,再由待定系数法求出反比例函数的解析式;
(3)把两个函数的解析式联立求出交点坐标,再结合图像可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的例题,再解答后面的题目.
例:已知x2+y2﹣2x+4y+5=0,求x+y的值.
解:由已知得(x2﹣2x+1)+(y2+4y+4)=0,
即(x﹣1)2+(y+2)2=0.
因为(x﹣1)2≥0,(y+2)2≥0,它们的和为0,
所以必有(x﹣1)2=0,(y+2)2=0,
所以x=1,y=﹣2.
所以x+y=﹣1.
题目:已知x2+4y2﹣6x+4y+10=0,求xy的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫作格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB'C′;
(2)画出△AB′C′向左平移4格后的△A′B″C″;
(3)计算线段AB在变换到AB′的过程中扫过区域的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,如何测得距离?
一位战士的测量方法是:面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。这是为什么呢?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知在数轴上有A、 B两点,点A表示的数是-6,点B表示的数是9.点P在数轴上从点A出发,以每秒2个单位的速度沿数轴正方向运动,同时,点Q在数轴上从点B出发,以每秒3个单位的速度沿数轴负方向运动,当点Q到达点A时,两点同时停止运动,设运动时间为t秒.
(1) AB=____ ;当t=1时,点Q表示的数是___ ;当t=___时,P、Q两点相遇;
(2)如图2,若点M为线段AP的中点,点N为线段BP中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由.若不变,请求出线段MN的长;
(3)如图3,若点M为线段的AP中点,点T为线段BQ中点,则点M表示的数为______;点T表示的数为______;MT=______ (用含t的代数式填空).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为打造书香校园,购进了甲、乙两种型号的新书柜来放置新买的图书,甲型号书柜共花了15000元,乙型号书柜共花了18000元,乙型号书柜比甲型号书柜单价便宜了300元,购买乙型号书柜的数量是甲型号书柜数量的2倍.求甲、乙型号书柜各购进多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】 我们定义:如图1、图2、图3,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB'C′是△ABC的“旋补三角形”,△AB′C′边B'C′上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.图1、图2、图3中的△AB′C′均是△ABC的“旋补三角形”.
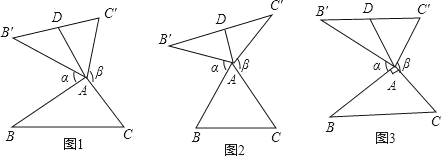
(1)①如图2,当△ABC为等边三角形时,“旋补中线”AD与BC的数量关系为:AD= BC;
②如图3,当∠BAC=90°,BC=8时,则“旋补中线”AD长为 .
(2)在图1中,当△ABC为任意三角形时,猜想“旋补中线”AD与BC的数量关系,并给予证明.
相关试题

